サッカーＷ杯、オーストラリア戦もクロアチア戦も力の入る熱戦でした。やはり体格が劣っているというのはツライですね。身長差もさることながら、日本人の細さ（体幹の細さ）が目立ちます。背は低くてもブラジルやアルゼンチンは体格的な不利を感じさせません。そういう意味ではアルゼンチンのサビオラなどは日本人のお手本となるようなとてもいい選手だと思います。

さて、速算の話です。といっても、私は計算がとても苦手でよく計算ミスをするのですが、少しばかり速算の方法をご紹介します。例えば「３４×２５＝？」という計算では「３４×１００÷４」と考えれば８５０となることが比較的容易に計算することができます。このように速算というのは直接に計算をするのではなく、少しの工夫で簡単に答えが求められる場合の計算方法をいいます。

そこで問題です。つぎの３問に共通の特徴を見つけて、簡単に計算をする工夫を考えてください。

• ３４×３６
• ６３×６７
• ４５^２

昨日の問題、

• ３４×３６＝１２２４
• ６３×６７＝４２２１
• ４５^２＝２０２５

についてです。この３問の共通点は「十の位が同じで、一の位の和が１０」、ということです。こんなとき、「十の位の数とそれに１を足した数の積」を上二桁に、「一の位同士の積」を下二桁にするとそれが答えになります(下図）。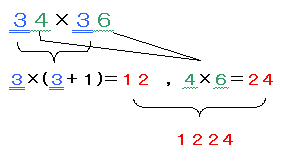

この３問以外でも「十の位が同じで、一の位の和が１０」であるような２数の掛け算ならこのやり方が使えます。この原理は説明すると分かりにくいのですが、下のようになります。

では、次のような問題ならどうでしょうか？

• ４３×６３＝
• ３６×７６＝
• ５３^２＝

あそびをせんとやさんに、おもしろいとコメントをいただきました。本当に嬉しいです。ありがとうございます。いつも「おもしろい」とか「不思議だなぁ」と感心させられているのは私の方です。今後もよろしくお願いします。

さて、昨日の計算問題です。

• ４３×６３＝２７０９
• ３６×７６＝２７３６
• ５３^２＝２８０９

これらは昨日のものとは逆で、「十の位の和が１０で、一の位が同じ」という共通点があります。この場合、どうなるのでしょうか？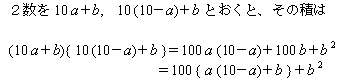

ということになります。これは、「十の位の数の積に一の位の数を足したものが上２桁、一の位の積が下２桁」ということを表しています。実際の計算では下のようになります。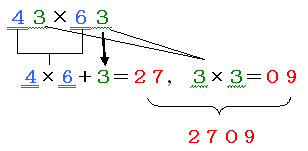

昨日、今日と紹介した速算の方法をちょっと応用すると次の計算もできるはずなのですが、いかがでしょうか。

• ３４×１３６＝
• ３６１×７６＝

昨日の問題です。３４×１３６については、３４×３６が１２２４なので、それに３４００を追加して４６２４です。３６１×７６については、３６０×７６が２７３６０なので、それに７６を追加して２７４３６です。少しだけ応用することで使うときの幅が広がります。

では、次の問題はどうでしょうか？

• １０６×１０８＝
• １１２×１０５＝
• ９８×９７＝

１００の周辺の掛け算です。

１００の周辺の掛け算では次のようになります。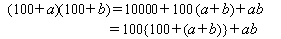

つまり、「それぞれから100引いた数を100に足した数が上３桁に、100引いた数の積が下２桁に」なります。具体的には下図をご覧ください。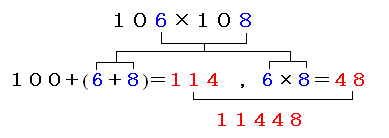

９８×９７のように１００よりも少し小さい数の積ならば、上式のa＝−２、b＝−３と負の数に考えれば同様に計算できます。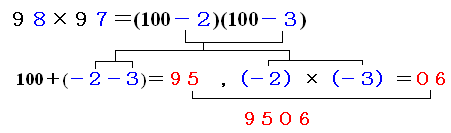

今回ご紹介したいくつかの速算法はコンピュータもびっくり！速算１００のテクニックから抜き出したものです。

今日は役場に書類をもらいに行かなければならないため１１時までお休みをもらったので、いつもより遅い更新になりました。決してＷ杯ブラジル戦の影響ではありません。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---