またもや毎度お世話になっているＧ先生からの出題。

トランプ５２枚を揃えて手に持つ。そのカードの一番上の１枚を捨てて次の１枚を残りのカードの一番下にもってくる、という作業を繰り返す。このとき、最後まで残っているのは最初の並びの上から何番目のカードか？

たとえば５枚のカード�@�A�B�C�Dでその操作を行うと、�@�B�D�C�Aの順に捨てられるので、答えは２番目ということになる。６枚のカードなら４番目だ。この問題は「継子立て（ままこだて）の問題」と言われる問題の変形だと思ったので検索してみると、「ヨセフスの問題」とも言われるようだ。実際にトランプでやってみれば答えはすぐに出るのだが、もっと違う枚数のカードだったらどうなるだろうか？

52枚のカードを上から１枚捨てて、次の１枚を一番下に、次の１枚を捨てて、次の１枚は下に・・・ということを繰り返すとき、最後に捨てるカードは最初の並びで上から何番目か？という問題。やってみれば分かると思うのだが、40枚目だ。これを一般化してｎ枚のカードでやってみたら・・・ということも面白いのだが、ｎの式で表すにはちょっとスッキリいかない（ので、ここでは書かない）。

ところでこのような一定手続きの操作なら、延々と繰り返していけば、いつかは最初の並びに戻るはずではないか、と思った。たとえば5枚のカード�@�A�B�C�Dでやってみると、

�@�A�B�C�D→�@�B�D�C�A→�@�D�A�C�B→�@�A�B�C�D

と、３回の操作で元の並びに戻る。これを周期３ということにする。カードが増えれば、当然周期も増えるだろうと思っていたのだが、意外なことにそうでもないのだ。たとえば10枚のカードなら周期は９なのだが、11枚のカードなら

�@�A�B�C�D�E�F�G�H�I�J
↓
�@�B�D�F�H�J�C�G�A�I�E
↓
�@�D�H�C�A�E�F�G�B�I�J
↓
�@�H�A�F�B�J�C�G�D�I�E
↓
�@�A�B�C�D�E�F�G�H�I�J

と、周期はたったの４なのだ。で、12枚のカードなら周期28と跳ね上がる。この周期を調べていくのも面白い（ので、調べた結果はまた次回）。

トランプ継子立てのつづき。前回提起した継子立てシャッフルの周期を調べてみた。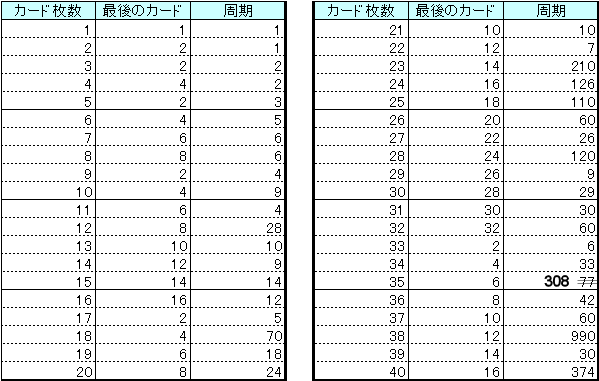

Ｃ言語でプログラムして、２回目、３回目・・・とシャッフルしたものを目視で確認したため、プログラムミスの可能性があり、目視での確認時の見間違いの可能性もあり、ちょっと信憑性の薄いデータです。何かミスがありましたらご指摘いただけるとありがたく思います。一応、Ｃ言語で作ったexeファイルをアップしときます（mamako.exe）。

ちなみにトランプの枚数５２枚だと周期は６４４。最初は実際にやろうとして３回目くらいですぐに断念したのだが、良い判断だった。４４枚だと１０００を超える周期になってしまって（たぶん）、そのあたりで調べるのを断念した。周期は大きくなる一方かと思うと、６５枚ではなんと周期７。法則をここしばらく考えてるんですが・・・。うーーーん、ひらめかない。年末というのに気持ち悪い。年越し迷宮入りとなってしまうのか？？？（つづかない）

先日の表に間違いがありましたので訂正します。３５枚の時の周期が３０８でした。すみません、そそっかしいですね。表の画像も訂正しました。

やはり目視確認には限界があるので、プログラムでチェックすることにした。最初はプログラムを考える方が面倒くさいと思っていたのだが、実際にやってみると最初からこうすればよかったなぁと反省した。目視による確認の方がよっぽど面倒くさいし、不正確だ。今まではとにかく紙と鉛筆で試行錯誤するしかなかったのだが、プログラミングを勉強し始めてから選択肢が広がったことがとても嬉しい。それで、ついでにカード１００枚までの周期表をあらためて掲載します。今度は間違いはないはずだ(と思う)。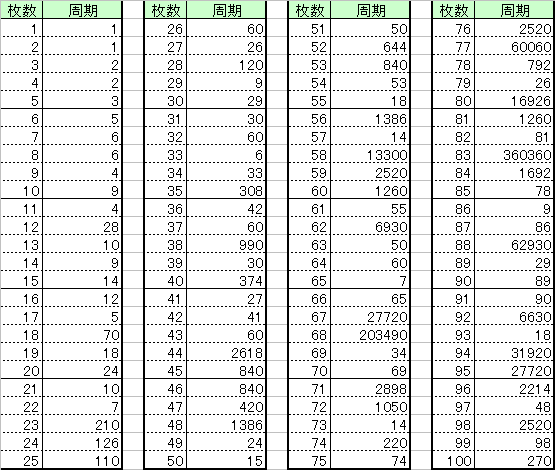

ちょっと気づいたのは、カードが5枚で周期３、9枚で周期４、17枚で周期５、33枚で周期６、65枚で周期７だから、129枚なら周期８、257枚で周期９、513枚で周期１０、1025枚なら周期１１・・・のはずだと思ってプログラムでチェックすると、その通りだった(プログラムはこちらmamako2.exe。前回のものではチェックできないので改善した。）。でも分かったのはそれくらいで、進展がない。
もうこのまま年を越そうと思います。それでは、よいお年をお迎えください。

昨年末の継子立てシャッフルを考えながら、もっと別のシャッフル方法でも規則正しく繰り返せばいつか必ず元の順番に戻るはずだと思って、別のシャッフル方法でも考えてみることにした。例えば、カードを２山に分けてパラパラと交互に噛み合わせるやつ（リフルシャッフルというらしい）だったらどうだろうか。これを完全に行うやり方をパーフェクトシャッフルというらしいが、つまり、カードを２等分してそれを完全に交互に噛み合わせるシャッフルを数回繰り返して元の順番に戻そうという考えだ。例によって、少ない枚数から考えてみた。
例えば４枚の場合、�@�A�B�C→�@�B�A�C→�@�A�B�Cと、２回で元に戻る。同様に６枚なら

�@�A�B�C�D�E
↓
�@�C�A�D�B�E
↓
�@�D�C�B�A�E
↓
�@�B�D�A�C�E
↓
�@�A�B�C�D�E

４回で元に戻る。８枚なら・・・・・意外にも（？）３回に減る。では、トランプ全部の５２枚なら何回で元の順番に戻るだろうか。（もしかして、マジシャンの世界では常識問題なのか？）

パーフェクト・シャッフル（カードを２等分して完全に交互に噛み合わせるシャッフル）によって何回の周期で元に戻るか、という問題のつづき。これもプログラムを作ってみた（pshuffle.exe）。前回、継子立てシャッフルの話題のときに、あそびをせんとやのhhaseさんからこのページを紹介していただき、自作プログラムのソースコードまで公開してくれました（12月29日のひとこと）。ありがとうございました。このプログラムを実行すると、私が作ったものよりも数倍速く答えを返してくれます。プログラミングの楽しさ、奥深さを感じました。今回のものも相変わらず単純なコーディングで進歩がないのですが、ぼちぼちと勉強していこうと思っています。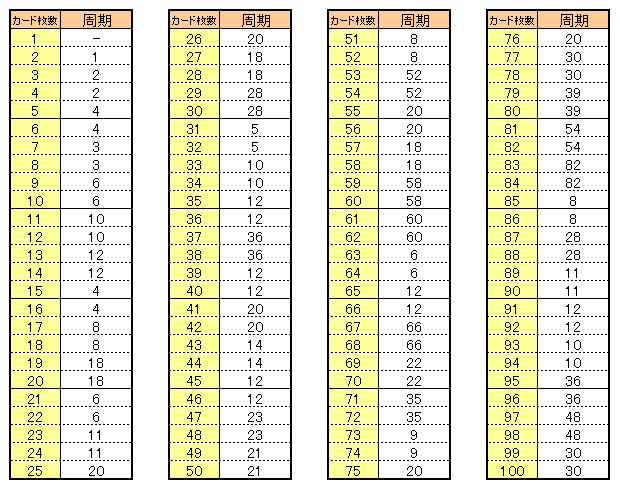
えっと、それでカード100枚までの周期表を掲載します。

奇数枚数の場合は、１を含む方を１枚多くして、その山から始めてその山で終わる、という具合に噛み合わせるとします。５２枚では８回というかなり少ない回数で元に戻る。実際にやってみようと思ったが、完全にうまく噛み合わせるだけの腕がないので断念した。
さて、この表の周期を見ると、奇数枚数とそれより一枚多い偶数枚数がペアで同じ周期であることが分かる。それ以外に、2n枚のカードのときに周期の規則はどうなっているのでしょうか？

あと２ヶ月ちょっとで、夢のような留学生活が終わってしまう。昨年４月当初には無限に感じられた時間が、あと２ヶ月か・・・と思うと少し寂しい。いや、かなり寂しい。すごく寂しい。光陰矢の如し、とは言うが、これほどとは思わなかった。あっという間のタメゴローだ。しかも、そろそろこの１年間のレポートをまとめなければならないのだが、当初思い描いていたことのどれほどもできていない。卒論制作に追われる大学４年生の気分だ。どうせなら、気分だけでも卒業旅行に旅立ちたいところだ。

さて、パーフェクトシャッフルの続き。カード枚数が偶数枚のとき、１枚目と最後のカードの位置は動かない。だからその最後のカードがなかった場合、つまりカード枚数が奇数枚のときも、１枚多い偶数枚のときとまったく同じ混ざり方をするのだ。詳しい説明は省くが、カードがｍ枚（ｍは偶数）とするとき、周期ｎは、２^ｎ≡１(mod m-1)を満たす数である。
たとえば、カード枚数が６枚なら、それから１引いた５で２のｎ乗を割った時に１余るような、そんなｎを探せばよい。この場合は、２の４乗の１６を５で割ると１余るので、周期は４ということになる。カードが８枚なら、２の３乗の８を７で割った余りが１だから周期３である。カード１０枚なら、２の６乗の６４を９で割った余りが１だから周期は６、という具合だ。

カード枚数が２のべき乗のときは周期が小さくなるのだが、トランプの５２枚は２のべき乗でもないのに周期が比較的小さい。８回のシャッフルなら念入りに混ぜているように見えるし、マジシャンなどの慣れた人ならできてしまうかもしれないですね。

MISDIRECTIONさんが、このところのシャッフルの記事について紹介してくれました（Unshuffled）。ありがとうございます。リンク先のYouTube動画もとても面白いので、ぜひご覧ください。私は何度も再生したり巻き戻したりして見てしまいました。正しくはパーフェクト・フェイロ・シャッフルというのですね。動画を見ているといとも簡単にやってるので、私も真似してやってみたのですがサッパリできません。それにしてもこういうアイデアを最初に思いついた人はスゴイと思います。

それでMISDIRECTIONさんご指摘のように、「継子立てシャッフル」（これはダウン・アンダーというのですね。勉強になります。）は実際にやってみようと思うと、場に捨てるカードを表に返して置かなければならず、私も違和感を感じていたところだったので、裏返しのままシャッフルできるように改めてプログラムしてみた（mamako4.exe）。前回の方法を正順、今回のものを逆順と呼ぶことにすると、逆順とは例えば５枚のとき、

�@�A�B�C�D
↓
�A�C�D�B�@
↓
�C�B�@�D�A
↓
�B�D�A�@�C
↓
�D�@�C�A�B
↓
�@�A�B�C�D

で周期は５となる。前回の正順と合わせて、カード100枚までの場合を表にしたので掲載します。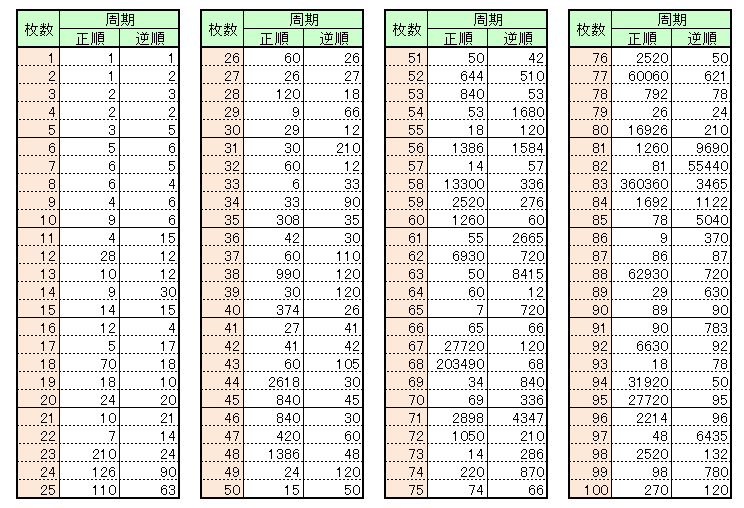

うーん。見えてこないす。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---