最近、面白い問題を見ましたので紹介します。

正十二面体のひとつの頂点�]をとる。一匹のアリが�]を出発し、正十二面体の辺上のみを歩き、�]以外の全ての頂点をちょうど一度ずつ通過して、�]に戻ってきた。アリの歩いた経路として考えられるものは何通りあるか。ただし、回転で重なり合うような経路や、道順が逆になっただけの経路も、異なるものとして数える。

これは先日開催された数学オリンピック予選の問題です。数学オリンピックとは高校生以下の数学好きな生徒を対象に行なわれる国際大会で、４０年前から開催されています。今年はスロベニアで行なわれるらしいです。対象が「高校生以下」なので高校数学までの知識ですべて解けるはずの問題が出題されるのですが、上の問題を見てもわかるように難問揃いです。
上の問題は予選の10番の問題ですが、いかがでしょうか。その筋の方には（どんな筋や）簡単に解けるものなのでしょうか？私なりのアプローチを試みて、何回かに分けてこの場で取り上げようと思います。

なかなかイメージがわかないので、正十二面体の図を作ってみました。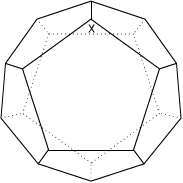

こんな図を見てもなかなか難しいです。実際私の場合、正十二面体の紙模型（だいたい手近に置いてあるのです）を見ながら考えたのですが、そんな立体図形を手にとって考えても一つの経路を辿ることもできませんでした。ひょっとしたら、そんな経路はないのではないか？とか疑ったりしたのですが、ちゃんと経路はあります。一例を掲載しますね。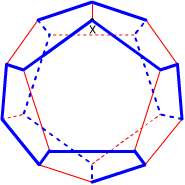

青の経路が一例です。逆回りも異なるものとして数えるので、これで２通りです。次回もこの続きを。

昨日のようにうまく図が描ければもしかすると何とかなるのかもしれませんが、フリーハンドで描こうとすると至難の業です。そこで、下図のようなものなら描けるのでは・・・と思って描いてみました。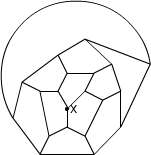

正十二面体とは似ても似つかないように見えますが、きちんと頂点は２０個、辺は３０本ありますし、一つの頂点に集まる辺の数は３本です。面が１１面しかないように見えますが、「囲まれた面」は１１個で「囲まれていない面」（図形の外側全部）が１個の計１２面ちゃんとあります。ただ、正五角形ではないし、外側の方の五角形なんてもう凸でもない、辺が曲線だ、などなど相当な無理があります。でも、この問題を考える時にはこの図で十分です。なんだかカブトガニみたいですね。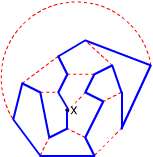
で、解答の一例を掲載します。

この図を見ながらだと、なんとなく解けそうな気がしてきました。次回へつづく。

昨日の正十二面体の平面モデルを見ていると、一筆書きの問題に見えてきます。ただし、「すべての辺を通って」という普通の一筆書きとは違って「すべての頂点を通って」元の位置に戻るという一筆書きです。スタートとゴールが一致する一筆書きで、しかも一つの頂点は一度しか通れないので、一つの頂点からは２本の辺しか出ることができません。つまり、頂点に集まる３本の辺のうち１本は使いません。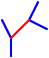
となれば、「どの２本の辺を通ろうかな」と考えるよりも「どの辺を使わないことにするか」ということを考えた方が考えやすいように思います。

で、上の図のように一本通らない辺（赤色）を決めれば、その両端から出る２本の辺（青色）は必ず通ることになります。それを考えながら、うまく数えていけば答えが出るはずです。

上のフラッシュ画像の再生ボタンを１度押すと頂点Xから赤い点線が一本出ます。この選び方は３本のどれを選んでも一様なので、後で３倍すればよいです。で、この赤点線が「使わない辺」を表しているとしますと、その両端の４本の辺は自動的に「使う辺」ということになります。でもフラッシュは自動的にはなってませんので（力不足でスミマセン）、もう一度再生ボタンをクリックしてください。
この状態で、次の「使わない辺」を選ぶときに場合分けが必要です。それぞれの青い辺の端から出ている２本の辺のうちの１本が「使わない辺」です。再生ボタンをクリックしてください。
仮に３のように選んだとしましょう。すると、次は自動的に青の辺が決まります。で、その後の番号４の時に次の赤い辺の選び方に場合分けが必要です。と言っても、そんなに多くはありません。
仮に番号５のように赤い辺を選んだとすると、あとは自動的に青い辺が決まり、一筆書きコースが完成します。

もうひとつ別のコースのものを作ったので掲載します。今度は２から３にいく時の赤点線の選択以降は一本道で決定します。

もっと鮮やかに計算でスパッと出せるものかもしれませんが・・・。私なりのアプローチということでこのような方法を紹介しました。次回は道順の一部を掲載します。

巡回コースの例を掲載します。昨日の平面モデルよりは正十二面体のイメージ図の方が見た目にわかりやすいと思いますので、そちらで作ってみました。

右と左で左右対称のコースになっています。これが「頂点Xから上向きの辺を使わない」ときのすべての場合です。その最初の使わない辺の選び方が３通り、それぞれのコースに右回りと左回りの２通りありますので、１０×３×２＝６０通りになると思います。

数学オリンピック予選の話に戻りますが、この手の問題１２問を３時間で解いて、今年の場合は７問正解で１次予選通過ということです。全問正解した者もいるというからビックリです。私のように手間ひまかけていては時間オーバーですね。もっともそれ以前に年齢オーバーでした。

正十二面体の辺に沿ってアリが歩く道順について考えてきました。一応答えは出たのですが、では他の正多面体だったら何通りになるのだろうか？と考えてしまうのは、自然の成り行きだと思います。そこで、問題を少しいじって以下のようにしたらどうなるでしょうか。

正多面体のひとつの頂点�]をとる。一匹のアリが�]を出発し、正多面体の辺上のみを歩き、�]以外の全ての頂点をちょうど一度ずつ通過して、�]に戻ってきた。アリの歩いた経路として考えられるものは何通りあるかを、それぞれの正多面体について考えよ。ただし、回転で重なり合うような経路や、道順が逆になっただけの経路も、異なるものとして数える。

・
・
・
・
・
・
・
・
・
・
少し間をあけて
・
・
・
・
・
・
・
・
・

正四面体の場合は６通り、正六面体の場合は１２通りになると思います。これらはひとつの頂点に３本の辺が集まっているところが正十二面体の場合と同じなので、同様の考え方で数えられます。では正八面体の場合はどうでしょうか？

・
・
・
・
・
・
・
・
・
またまた間をあけて
・
・
・
・
・
・
・
・
・

これはひとつの頂点に４本の辺が集まってくるので少し面倒です。集まる辺が３本のときは「使わない辺」を考えましたが、４本になると「使う辺」を考えても「使わない辺」を考えても労力は同じように思います。むしろ「使う辺」を考えた方がストレートで考えやすいでしょう。

隣り合う２辺を使う場合・・・・・

この３通りに、隣り合う２辺の選び方４通りと、逆順の２通りを掛けて３×４×２＝２４通り。

隣り合わない２辺を使う場合・・・

この２通りに、隣り合わない２辺の選び方２通りと、逆順の２通りを掛けて２×２×２＝８通り。で、合計３２通りになります。

正二十面体の場合ですが、何とかして答えを出せないものでしょうか？

	アリの経路	頂点	面	辺	ひとつの頂点に 集まる辺の数
正四面体	６	４	４	６	３
正六面体	１２	８	６	１２	３
正八面体	３２	６	８	１２	４
正十二面体	６０	２０	１２	３０	３
正二十面体	？？？	１２	２０	３０	５

正二十面体は、もうお手上げです。時間があるときにゆっくりと考えたいと思います。オイラーの多面体定理みたいにスパーっと出てくると気持ちいいのでしょうけれども。もし何かお気づきになりましたらご連絡をいただければ嬉しいです。

記述に間違いなどがありましたら遠慮なくご連絡をいただければとてもありがたく思います。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---