今日からちょっと変わった別の物体を紹介します。下の写真を見てください。

青と赤の立方体がそれぞれひとつずつ、なにか怪しげな切れ目が入っています。これ、実は輪ゴムでとめていまして、そうしていないとバラバラに崩れてしまうのです。さて、そこで問題ですが、バラバラになった後のパーツというかピースはどんな形をしているでしょうか？つづきはまた明日。

昨日の立方体、輪ゴムをはずして形を崩すと下の写真のようになります。

裏には別の色をつけています。

これは下図の赤い線で囲んだ四面体を２４個つなげて作ったリングです。これもカライドサイクルの一種と言ってよいかと思います。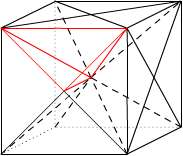

こんなにたくさんつなげると、前回紹介したカライドサイクルのように「クルクル回ります」と言っても「当たり前じゃん」という感じです。と考えると、前回のものは閉じるときと開くときを繰り返すギリギリの感じを不思議に思ったのでしょうね。今回のもののように開きっぱなしでは不思議でも何でもないですね。

このリングを「カライドキューブ」と名付けようかと思ったのですが、すでに「カレイドキューブ」という物があるそうですので、「k-cube」と呼ぶことにします。で、このk-cubeは組み方によって立方体以外の立体に変容します。つづきは次回に。

四面体を２４個つないだk-cubeのつづきです。２つを組み合わせると下のような立体にもなります。

	まず２つのk-cubeを揃えます。 前回紹介した四面体を２個 合わせてつなげたカライドサイクルができます
	うまく組んでいくと菱形十二面体ができます。
	さらに、またばらして組みなおしていくと、
	先程とは違った色の菱形十二面体ができます。 で、外側のk-cubeだけはがしていくと
	中には立方体が隠れていました。
	もう一度組みなおしていきますと、
	また別の色の菱形十二面体ができました。
	これも外側だけはがしていくと中には立方体が隠れています。

立方体をもうひとつのk-cubeで包むことにより菱形十二面体ができます。２つのk-cubeの立場を入れ替えれば別の色のk-cubeが作られます。また２番目の画像のように、２つが混ざったような菱形十二面体もできますので、今回の方法では合計３つのパターンで菱形十二面体に組むことができます（別の方法ならもっとたくさんのパターンで菱形十二面体ができます）。

次回はk-cubeの作り方を説明したいと思います。

今日はセンター試験です。受験生には普段の力をしっかり出し切ってほしいです。

k-cubeの展開図です。展開図といってもカライドサイクルのときのように一枚紙ではなく、バラした時の四面体ひとつ分です。PDF版はこちら。PDF版は６枚印刷して作成してください。

左の画像で、青い三角形が２：(ルート２)：(ルート２)の直角二等辺三角形、紫の三角形が２：(ルート３)：(ルート３)の二等辺三角形、緑の三角形が１：(ルート２)：(ルート３)の直角三角形です。以前も掲載した下の図をイメージして作りました。

これを一つ作るのは何てことはないのですが、一つのk-cubeには２４個必要ですし、二つ作るには４８個作らなければなりません。かなり根気の要る作業です。
つなげる時は、一番長い辺（２の長さの辺）同士と、一番短い辺（１の長さの辺）同士をつなげます。セロハンテープで表裏の両方から止めるとよいです。

カライドサイクルのようにつながった形で展開図が描けないかな、と考えて描いてみたのが下の図です。これを４枚つなげて一つのk-cubeができるはずです。破線の部分は切ってください。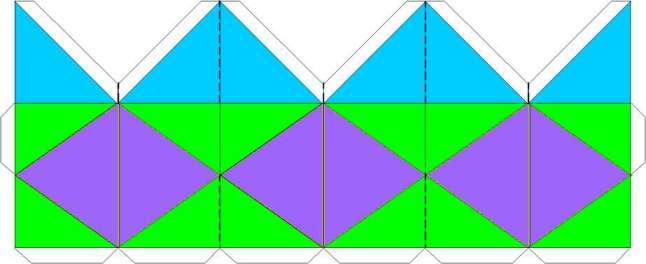

吉本キューブやカライドサイクルもそうなのですが、このk-cubeも内側のものが変形後には外側になったりするため、かなりキッチリ作ったつもりでも組み合わせた時にどうしても隙間ができてしまいます。仮に片方を少し小さめに作れば確かにきれいに収まるのですが、内側と外側を逆転させると全く収まらなくなってしまってうまくいきません。

k-cubeの最終回です。以前に「別の方法ならもっとたくさんのパターンで菱形十二面体ができます」と書きましたので、その「別の方法」を掲載します。

２つのk-cubeを組み合わせないで、それぞれが菱形十二面体の半分の形を作ることができます。上の写真では４面が緑色、４面がピンク、４面が半分半分になっています。

今度は切断面が平面ではなく、ギザギザになっています。３面が緑、３面がピンク、６面が半々です。

上の写真では６面が緑、６面がピンクで、半々の面はありません。

これは最初と同じように切断面が平面です。が、切断の仕方に違いがあります。５面が黄色、５面が紫、２面が半々です。

これらの他にもまだk-cubeには何らかの秘密が潜んでいるかもしれません。また、４面体のつなぎ方を変えたり、立方体の分割方法を変えたりしたら、もっと面白いことがあるのかもしれませんが、k-cubeについてはこれでひと区切りにします。

２２日はサッカー部の新人大会がありました。私の前々任校との対戦で、教え子の後輩が指揮を執っているチームだったのですが、延長の末２−３で負けました。両校の選手とも精一杯の力を出し切った好試合だったと思います。私も非常に疲れました（その前の試合で線審をしたりしたので）。もう"年"ですね。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---