今日から何回かに分けて「カライドサイクル」について紹介したいと思います。私が紹介するまでもなく知ってる人は知っているだろうし、知らない人も興味がないかもしれませんが、所詮は「ひとりごと」ですから。「ひとりごと」を盗み聞きできる･･･ということには興味がある、という方もいるかもしれないし。

「M.C.エッシャー　カライドサイクル」というクラフト本です。そもそもカライドサイクルとは、四面体をいくつか辺と辺をつなげて作ったリングのことですが、この本はそのカライドサイクルにエッシャーのデザインを印刷して本にしたものです。中には、丁寧で分かりやすい解説が40ページほど載せられているのですが、カライドサイクルの展開図を印刷した厚紙も挟み込まれているので実際に作ることができます。それでいくつか作ってみました。

上段の２つが四面体６個をつなげてできたカライドサイクルで、下段の２つが８個をつなげてできたものです。これがクルクルと回転するのです。回転するといっても右回りとか左回りではなく、中心を下から押し上げるとだんだんと中心部が開いていき外側へ、同時に下からは新たな中心が現れて、・・・という具合に回転します。ミカンの皮をむくようなイメージ・・・と言うと逆に分かりにくいですね。またいずれパタパタFlashか動画にして紹介します。

四面体６個からなるカライドサイクルの展開図を下に掲載します。PDF版はこちら。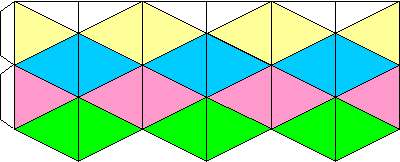

斜めの線を山折に、縦の線を谷折に折り目をつけます。

頂点を下からポコポコっと突いて、ヘビのように丸めます。

白い部分がのりしろですので、糊付けします。

ヘビの頭と尻尾をつなげてリング状にして糊付けします。この部分は弱いのでテープで補強した方がよいです。

２：（ルート５）：（ルート５）の二等辺三角形四面からなる四面体が６個つながったカライドサイクルです。
立体そのものも面白いですが、この展開図もすごいです。私が考えたなら四面体６個ばらばらに作ってつなぎ合わせてしまうところです。

エッシャーのカライドサイクルをデジカメ動画にしてみました。

四面体６個のカライドサイクル(94KB)

1958年にグラフィックデザイナーのウォレス・ウォーカー（Wallace Walker）が、Iso Axis（アイソアクシス「回転するジャバラ」）を発見しました。その動画もついでに。

アイソアクシス(100KB)

「エッシャーのカライドサイクル」によると、カライドサイクルはこのIso Axisのひとつということです。さらについでに、８個の四面体からなるカライドサイクルの動画も。

四面体８個のカライドサイクル(94KB)

昨日は地元で成人式があり、式の後サッカー部の新成人のＯＢが集まって現役チームと練習試合をしました。こんなときに教員をやっててよかったと思える醍醐味のひとつです。

いよいよ３学期が始まりました。正月前後はゆっくりできたものの、この冬休みも忙しかったです。でもこのサイトを知っている知人には、いくら「忙しい」と訴えても信じてもらえません。

さて、カライドサイクルの続きです。今日は「invertible cube」を紹介します。

⇔

⇔

上図のような感じで、少し細長い四面体６個がリング状につなげられたものを「invertible cube」といいます。1928年にPaul Schatzによって考案されたそうです。図だけではわかりにくいので動画にしました。

invertible cubeの動画

海外のサイトですがこちらはすごいです。が、かなり重たいサイトなので遅い回線の方は避けた方がよいです。こういうのを見ると「LiveGraphics3D」というのにも興味がわいてきます。忙しくなくなったら挑戦したいと思います。（定年後だな）

invertible cubeの展開図を掲載します。PDF版はこちら。PDF版では用紙の効率を考えて2段にしています。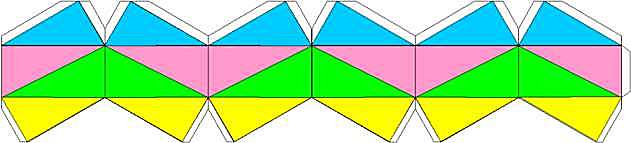

1：2：(ルート3)と1：2：(ルート5)の２種類の直角三角形からなる四面体６個からできています。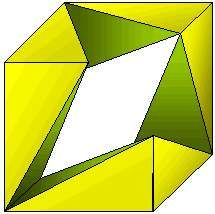

回転している最中に一瞬だけ立方体の一部の形になります。それで「cube」と名がついているのでしょうね。

あそびをせんとやのhhaseさんに<おまけのひとこと>をいただきました。お気遣いいただきありがとうございます。「いくら『忙しい』と訴えても信じてもらえません」というのは実は正確な表現ではなく、「いくら『忙しい』オーラを発しても誰も気づいてくれません」というのが正しいです。私の存在すら気付いてないかもしれません。こうなったら『忙しいオーロラ』を発するしかないのか（どんなんや）。最近、実際に「忙しい」と言葉で発したのは、妻から「年末くらい掃除をしたら」と言われたときくらいです。
無理をせずにぼちぼちとやっていこうと思いますので、今後もよろしくお願いします。

さて、昨日の続きです。invertible cubeをクルクルまわして遊んでいたら、ちょうど正三角形になるときと、正三角形の穴が開くときがあることに気付きました（何のオーラも発していないくせに気付いてもらえるとは幸せなやつだ）。

⇔

同じものを２つ作って、はめてみたのが上の写真です。ちょうどぴったりとはまって手にとってみると、それを回したくなるのが自然のなりゆきと思うのですが、とにかくやってみましたらこれが２つ重なったままクルクルと回るのです。動画を掲載します。

invetible cube２個重ね(104kb)

これはまた別の形のカライドサイクルができました。で、もうちょっと続きがありますがそれは明日にします。

いろいろ事情があって一日更新が遅れました。これで私がいかに忙しいかが証明できたと思います。さて、前回２つ重ねのinvertible cubeを紹介しましたが、それをクルクル回して遊んでいると、再びひらめきました。正三角形になるときと正三角形の穴があくときがこの場合もあるのです。１月１２日(一昨日)に掲載した動画で確認してみてください。動画では、ピンクの三角形ができるときと、ピンクの枠ができるときがあることが確認できると思います。そこで、あと２つ同じinvertible cubeを作れば合体できるのではないか・・・と思って、実際に作ってみました。

で、これが４個合体したまま回るんです。動画も作成しましたのでご覧ください。

invetible cube４個重ね(98kb)

お気づきの方もいらっしゃると思いますが、これは１月９日に紹介した四面体６個のカライドサイクルと相似形です。逆に、この四面体６個のカライドサイクルを４分割したものがinvertible cubeである、とも言えます。
となれば、あれはどうなるのでしょうか・・・？続きは次回に。

四面体６個のカライドサイクルを４分割してinvertible cubeができるのなら、四面体８個のカライドサイクルを４分割したらどうなるのでしょうか。
実際に作ってみました。作り方はまた後日紹介したいと思います。

⇔

前回は正三角形とその枠ができましたが、今回は正方形とその枠ができます。動画も作成しました。

right-angled kaleidocycle of order 8(91kb)

以前も紹介した海外サイトのこちらに「right-angled kaleidocycle of order 8」と紹介されているので、そのまま引用しました。こちらのサイト、前回は「重い」と書きましたが重いのはJava Appletを読み込む重さのようで、回線の遅さとは関係ないかもしれません。「LiveGraphics3D」というソフトで作成しているようですが、とてもすごいです。マウスポインタをのせるとアニメーションを開始し、左ドラッグで自由に回転させることができます。右ドラッグすると線や面を消すことができるし、Shiftキーを押しながら上下に左ドラッグすると拡大・縮小できます。こういう表現方法ができるといいなあといつも思うのですが、力及びません。定年後に頑張りたいと思います。

２つ重ねて回してみた動画も掲載します。

「right-angled kaleidocycle of order 8」２個重ね(103kb)

こんなに動画ばかり掲載して、私のサイトの方が重たいかもしれないですね。

４つ重ねて回してみた動画も掲載します。

「right-angled kaleidocycle of order 8」４個重ね(96kb)

下は「right-angled kaleidocycle of order 8」の展開図です。PDF版はこちら。PDF版は例によって２段にしています。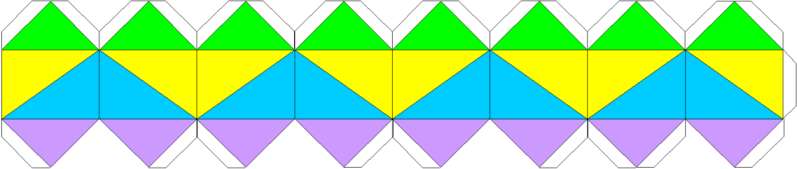

１：１：（ルート２）と１：（ルート２）：（ルート３）の直角三角形からできています。この立体は非常に面白くて、以前こちらでも紹介した吉本キューブにも関連してきます。吉本キューブにはNo.1からNo.3までの３種類があるそうで、そのNo.2だかNo.3だかにとてもよく似ています。No.2やNo.3は私も写真でしか見たことがなくてよくわからないまま書いているのですが、その辺りの話は次回にまわしたいと思います。

昨日は妻の誕生日で、ケーキを買ってみんなで食べました。ケーキを切りながらあそびをせんとやさんの「公平に分ける話」を思い出しました。我が家の場合は・・・、と言い出したら非常に特殊な話になって一般性のかけらもないのですが、基本的には私が切り分けて、選ぶときにジャンケンします。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---