今日は簡単な更新です。遅刻しそうなのです。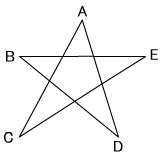

上の図で∠A＋∠B＋∠C＋∠D＋∠Eは何度でしょうか。よく見かける問題ですみません。

花粉症の季節になって、毎年のことながらウンザリしています。昼間よりもむしろ夜眠っている時に鼻が詰まって熟睡できないことの方がつらいです。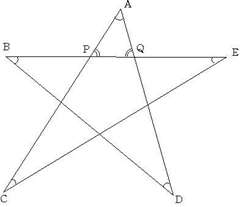

三角形の外角は他の二つの内角の和に等しいので、∠P＝∠C＋∠E、∠Q＝∠B＋∠Dです。△APQにおいて∠A＋∠P＋∠Q＝180°なので、結局
∠A+∠B＋∠C＋∠D＋∠E＝180°になります。

これはよく見かける問題だと思います。では、下の図で∠A〜∠Gまでの和はそれぞれ何度でしょうか。

今日は卒業式です。でも、まだ進路が確定していない者もいて、感慨に浸ってばかりもいられません。

昨日の角度の求め方でも何とかできるかもしれませんが、なんだか図がゴチャゴチャして混乱してしまいそうです。そこで、別のアプローチをしてみます。昨日の右図で説明します。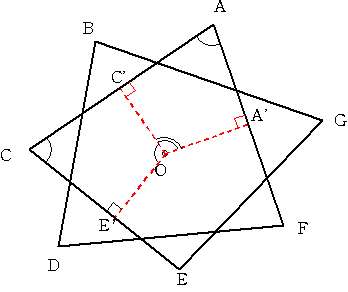

上図はグラウンドに大きく図を描いてみたとして、真ん中辺りの点Oに私がいるとします。次に友人のヒトシくんに点A'から線に沿って点Aの方向に動いてもらいます。このとき、私はヒトシくんを目で追いかけます。実際は目だけではなく体ごとヒトシくんの方向に向けてその場で回転するように追っていきます。つまり、私は最初A'の方向に体を向けているのですが、ヒトシくんが動くにつれて点A'→点A→点C'へと体の向きが変わっていくとします。
ヒトシくんがA'からC'まで動いた時に、私は∠A'OC'の角度だけ回転したことになります。四角形OA'AC'で考えれば四角形の内角の和が３６０°で、９０°を２箇所使っていることから∠A'OC'＝180°−∠Aという式が成り立ちます。同様に、ヒトシくんがC'→C→E'と進むと、私は∠C'OE'＝180°−∠Cだけ回転します。これを同様に繰り返して最初のA'にヒトシくんが戻ってきた時には、私はその場で２回転しているはずですから、720°回転したことになります。これを式で書くと、

(180°−∠A)＋(180°−∠C)＋(180°−∠E)＋(180°−∠G)＋(180°−∠B)＋(180°−∠D)＋(180°−∠F)＝720°

これを計算すると、∠Aから∠Gまでの和は540°と言うことになります。

この考え方を使うと昨日の左側の問題も、和が180°という答えが出ると思います。では、下の問題はどうでしょうか？∠A〜∠Iの大きさの和を求めてください。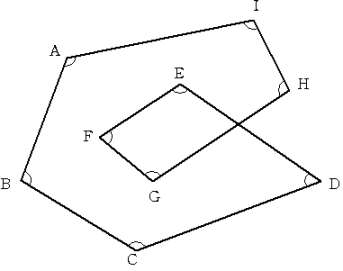

あそびをせんとやさん、いつも訪問していただいてありがとうございます。「さてどんなふうに話はまとまるのだろう」とは奇遇ですね。私も同感です。あまり後先考えず、いつもの調子でぶちまけてしまった次第です（お恥ずかしい限りです）。民主党の永田議員の心境です。こうやって時間を稼いでいる間に、何か画期的なことをひらめかないかな、と思っているのですが。。。今となっては「ぶちまけたのが国会でなくてよかった」と思うようにしています。

あそびをせんとやさんの「ppバンド多面体」、おもしろそうですね。何よりもお金がかからなそうなところが私向きのテーマです（山本さんの割り箸コースターも！制作費８０円というのもスゴイ）。こんなおもしろいものを数年前に作っておいてストックしておくあたりがすごいと思います。

さて、本題に戻って何とかしてまとめなければ！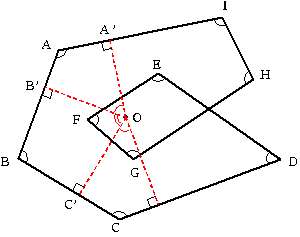

前回と同様に考えてできる問題なので、
(180°−∠A)＋(180°−∠B)＋・・・＋(180°−∠I)＝７２０°を計算して、∠Aから∠Iまでの和は900°です。

でも次のような図だったらどうでしょうか？∠Aから∠Lまでの大きさの和を求めてください。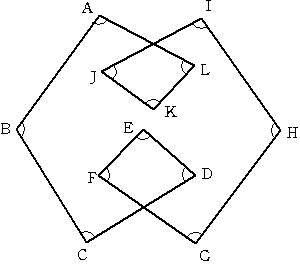

卒業式の日の話ですが、サッカー部では後輩が記念のマスコットボールに寄せ書きをして卒業する先輩に贈るのですが、なんとその後に「それじゃ、これは俺たち（卒業生）から」と言って、私にこんなものをプレゼントしてくれました。

小さい方には寄せ書きをしてくれています。本当に嬉しかったです。

昨日の朝、職場に兄から電話があり、「答えが違ってるよ」と。よく考えると１０直角を1800°としていました。持つべきものはよい兄弟ですね。ありがたいです。しかし、職場からアップロードができず、訂正できたのは昨夜９時くらいでした。その間にご覧いただいた方にはご迷惑をかけました。今後も間違いが多々あると思いますが、気軽にご指摘いただけるととても助かります。
授業中に計算間違いをした時には、「もちろん君らを試したのだ。間違いに気付かなかった人は恥ずかしいと思いなさい。」とか言ってはぐらかすときがあるのですが、ここだとそうもいきませんね。「間違い探し」の要素も合わせて、気軽に楽しんで見ていただけるとありがたいです。

昨日の２回ループの問題です。一昨日の考え方を使うとすれば、下図のように変形して２重ループにするとできます。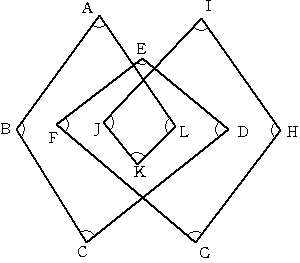

「180°×12頂点−(和)＝360°×3回転」だから、(和)は12直角で1080°になります。でもこんなに大胆に変形しても和は保たれるのか、という大きな問題が残ります。ちょっと暗算で考えようと思う分にはこの方法は有効かもしれませんが（暗算でやってるとまた間違えてしますのですが）、中・高生に説明するには無理があります。説明する時は次の図の方が良いかもしれません。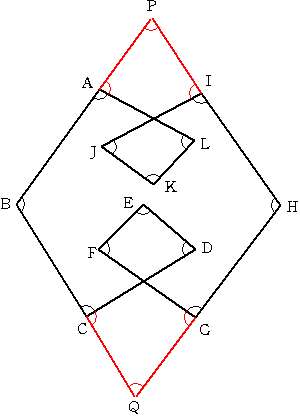

四角形PBQHの内角の和360°に、点A,C,G,Iにできる180°×4を加えて1080°です。

で、その・・・、まとめというか、落としどころというか、特に落ちはないのです。その点においてアンガールズみたいです。「ジャンカジャンカ」言いながら幕を閉じたいところです。実は苦し紛れにここで作った爪楊枝みたいに立体になると角度はどうなるのか、と思ったのですが、自由度が高すぎてどうにでもなるようです。次に考えたのが、三角形の内角の和が180°であるように四面体の各面のなす角には何らかの縛りがあるのではないか、ということです。ある２つの面のなす角が大きかったら他の面のなす角は小さくなるように思うのですが・・・。立体になると途端に難しくなります。もうちょっと考えて何か思いついたらまたここに書きたいと思います。何かヒントなどご教授いただけるととても嬉しいです。

ろくはロッパの･･･さんが、見事に落としどころを見繕ってくれました。ありがとうございます。なるほど、外角に目をつけるのですね。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---