５年ほど前、数学者の秋山仁先生の講演を聴く機会があり、その中で興味をそそられる話がなされていたのでここで紹介します。まず、下のFlash画像を再生してみてください(正方形の左上のボタンをクリックしてください)。

赤枠の正方形が青枠の正三角形に変身しました。温泉宿などにあるタングラムパズルのようですがこの図形にはちょっと制限があって、辺か頂点上に蝶番のように可動だけど離れない点があり、そこをハトメパンチで固定したようにしてクルクルと変形していきます。これをハトメ返しというそうです。この正方形⇔正三角形の変形は天才パズリスト・デュードニが「カンタベリーパズル」の中で紹介したのが最初だそうで、秋山先生はこの図形分割のことを「デュードニ分割」と呼んでおられました。詳しくはこちら「知性の織りなす数学美」(秋山仁著)をご覧ください。

さて、このカンタベリーパズル、どのような比で分割すればうまくできるのでしょうか？

自宅に戻ってこのページの更新作業を使用と思ったら、なんとカウンターが倍増していました。昨晩が５０くらいだったのに今は１００を越えています。これまで２〜３人にしかURLを教えていなかったので、毎日カウンターは２〜３ずつしか増えていませんでした。２０日くらいかけて５０（というのも情けない話ですが・・・）だったのに、１日にして倍増！びっくりしました。
が、その後「あそびをせんとや」さんのページを見て納得しました。なんと、「あそびをせんとや」さんのページでここを紹介してくれていたのでした。ありがとうございます。これからも一層（でもぼちぼち）がんばるぞ！とファイトが沸いてきました。「あそびをせんとや」さんからお越しの皆さん、はじめまして。今後もどうぞよろしくお願いします。

昨日のハトメ返しの続きです。５年前初めてこの図形を見た後、自宅に戻ってから自分で作ってみようと思って厚紙で作ったのが左下の画像です。右の画像（昨日のものを再掲）と比べてみてください。

４辺とも中点をとって分割してみたら、このようなものができました。最初は「できた！」と思ったのですがどうも様子がちがう。よく見ると正三角形でなく二等辺三角形になってしまいました。三角形のときの赤い切れ目も、講演会で見たときは段差があったはずなのにこれは十字になっています。そこで、色々と考えたあげくに出た答えのみ掲載します。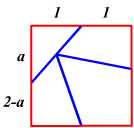

上図のように正方形の一辺の長さを２とすると、上下の辺は中点で分割されることになります。左の辺を図のように分割したとすると、

	となります。で、これは
	と非常に似通った数字です。

上の式は正確な値でそれはそれで価値のあることなのですが、実際に作図したりするときに使える数字は下の式です（作図誤差の範囲としました）。一辺の長さが２なので結局左の辺を４：３に、右の辺を３：４に分割した点を利用すればよいです。

計算して上の値が出た後何か簡単な比にならないかと考え始めたら、すぐにこの比が見つかりました。こんな簡単な比の近似値が存在するのも不思議な感じを受けました。

簡単なハトメ返しの例をいくつか作ってみました。

「あそびをせんとや」さんでバージョンアップされた「キングと悪魔のパズル」の「思考ルーチン視覚化アプレット」を作者のhhaseさんからいただきました。ありがとうございました。これ、ホントにすごいです。次は出来るだけ少ない手数で勝てるように挑戦してみたいと思います。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---