昨日、小４の二男が「僕、歌を作った」と言って、突然歌いだした。出だしの歌詞は、「♪いいことなくても幸せなんだもの〜♪」
とても短い歌だったが泣けました。
さて先日の問題

「２００７」を１から８までの連続する自然数の四則演算で表してください。（）は使ってよいが、順序は１〜８を崩さないとします。

この解答例は次のカッコ内をドラッグしてください。「１＋２×｛３＋４×５×（６×７＋８）｝」この他にも正解があるかもしれません。
この解答を考えるときにWindows付属の電卓を使用しているのですが、その他にどうしても素因数分解をすることが多くて困ったので、ちょっと自分でプログラムをしてみました。「2500までの素因数分解プログラム」。問題の性質上2500までの素因数分解ができれば十分だろうということで、50までの素数15個を使って計算しています。だから2809（＝53×53）を入力すると素数と判断してしまうのですが、それより小さい数なら大丈夫だと思います。では、ちょっと早いですが2008年を迎えるということで、2008年問題。

「２００８」を１から９までの連続する自然数の四則演算で表してください。（）は使ってよいが、順序は１〜９を崩さないとします。

1＋{(2−3＋4)×(5＋6)×7−8}×9

これを考えていると「なんだ、１から８までの数でできるじゃん」という方がいるかも知れないので、続けてもう１問。

「２００８」を１から８までの連続する自然数の四則演算で表してください。（）は使ってよいが、順序は１〜８を崩さないとします。

[1＋2×{3×4×(5＋6)−7}]×8

もしよければ「2500までの素因数分解プログラム」を使ってみてください。もし問題があればご連絡いただけるとありがたく思います。

先日の「2500までの素因数分解プログラム」はＣ言語で作ったのだが、今回はJavaアプレットにしてみた。

最近ようやくＣ言語には慣れてきて、非常に簡単なプログラムなら多大な時間をかけて作れるようになった。だから先日のものはなんてことはなかったのだが、今回のJavaアプレットは初めての挑戦で、分からないことだらけだった。Ｃ言語とJavaでは作法がずいぶん違うのだ。本当は「2008年問題」出題の時にこのようにホームページ上で計算するようにしたかったのだが、その時はうまく動作しなかった。ここ２日間、試行錯誤を重ねて、やっとの思いで作ったのがこんなチッポケなものだ。プログラマというのは割に合わない職業だと聞いたことがあるが、その一端を垣間見た気がした。このアプレットも試行錯誤を繰り返したため、錯誤したままかも知れない。もし何か間違いがありましたら、ぜひご連絡ください。（連絡先）

またまたＧ先生が面白い問題を持ってきてくれた。問題は以下の通り。

任意の凸四角形の内部に１点を取り、その点と各辺の中点を結んで４つの四角形に分割する。これをハトメ返しにすると新たな四角形ができるが、新たな四角形が平行四辺形になるようにするには、凸四角形内のどこに点をとればよいか。

言葉で書かれても分かりにくいと思うので、以前作ったハトメ返しを思い出してFlashで作った。

最初の黒い四角形はどんな四角形でもよいとして、赤い四角形が平行四辺形になるような分割の仕方を考えろ、という問題。この図の例では適当に点をとったため平行四辺形にはなっていないが、どうすればよいでしょうか。

先日出題したハトメ返しの問題について、ひねもすあそびのおかちゃんさんからコメントをいただきました。ありがとうございます。「ひねもすあそび」12/9更新の物体は「Move Form」ですね。これもいつか作ろうと思いつつ棚上げにしているものの一つです。実際に手にしてみないと、この面白さは分からないんだろうな、と思います。冬休み中にでも子どもと一緒に作ってみようかと思っています。

さて、前回のハトメ返しの問題は「平行四辺形を作れ」ということだったので、その答えのFlashを掲載します。

この問題は「四角形の内部の一点から」という制約がついていましたが、この制約を無くして、「四角形の各辺の中点を通る線分で四角形を４分割して、平行四辺形に変形するハトメ返しを作れ」ということにしたらどうだろうか？下の再生ボタンをクリックすると解答例のFlashが表示されるので、自分で考えてみようという方はご注意ください。

ではこのような方法（「内部の１点から」という制約がない方法）で、台形を作るにはどうしたらよいでしょうか。また、長方形を作るにはどうしたらよいでしょうか？

最近、アクセス解析を乗り換えようかと思って２種類目のアクセス解析をかけたのだが、昨日チェックしてみると海外のリンク先からこちらに来られている人がいるようなので、ちょっと探ってみた。すると、こちらのページKaleidocyclesから来ているようだ。英語で書かれているのでサッパリなのだが、写真や挿絵がとてもきれいで興味深く眺めていたら、なんと！一番下の方に私のサイトへのリンクが貼られているではないか！いやはや、いよいよこのページもインターナショナルだ。インターネットってほんと凄いんですな。ビックリしました。
それにしてもそのページは恐らくドイツの方が書いていると思うのですが、メインページから辿るたくさんのページがどれも面白そうです。何書いてるのか分からないのがつらいところだが、絵を見ているだけでも面白いということだけは分かります。

さて、先日の台形と長方形の問題の解答例。下の左が台形で、右が長方形です。再生ボタンをクリックするとアニメーションが始まります。

平行四辺形に比べて、台形は条件が緩くて長方形は条件がきついです。では同じようにハトメ返しを作って菱形にするにはどうしたらよいでしょうか？

菱形の解答例です。

左が前回までのものと同じ形の四角形からスタートしているのですが、平行四辺形のときに比べてどの条件が加わったのでしょうか。参考までに、右に全く別の四角形からスタートしたものも付けました。

金曜日は２週間ぶりの病院に行く日で、膝を診てもらった。ちょっと水がたまっているとのことで、水を抜いてもらうとともにヒアルロン酸を注入してもらった。このところ回復しているという実感もなく、相変わらず走ると痛いし無理はできない状態だ。日常生活に支障はないものの、ジョギングなどもできないためこのところ運動不足で、食べる量は以前と変わらず何でもよく食べるため、体重が増加傾向だ。このままクリスマスと正月を迎えるのは危険な香りがする。体重増加→膝への負担増加→左膝の回復が遅れる→左膝をかばう→右膝の負担増加→右膝負傷→運動制限→体重増加、というレインボー・サイクルに突入しかねない。レインボー・サイクルとは七色循環の英訳であり、何だかこうすると苦しいことも楽しそうにみえるかなと思ったのだが、ただ面倒くさいだけだった。人生初の食事制限をすべきかどうか、ポテチを食べながら悩んでいるところだ。

さて、ハトメ返しもそろそろ飽きてきたとは思うのですが、せっかく作ったものがあるのでそれを全部吐き出して終わりにしたいと思う。全部吐き出すと、少しは体重も軽くなるような気がするし。
で、前回までと同様に四辺形の各辺の中点で分割するハトメ返しで、今度は三角形を作りたい。下の再生ボタンをクリックしてみてください。

では二等辺三角形にするにはどのように分割したらよいでしょうか。また、直角三角形にするにはどのようにしたらよいでしょうか。

下の左が二等辺三角形、右が直角三角形の例です。「ポーズボタン」がうまく作動しないのですが（スミマセンm_ _m）、ボタンをクリックしたままボタン外へドラッグして離すと一応止まります。再びポーズボタンをクリックすると再開しますので、面倒ですがそれでやってみてください。

二等辺三角形にしても直角三角形にしても、ここに載せたものだけが正解というわけではなく他にも正しい答えはあるので、それを探すのも楽しいかもしれない。今回は一般の四辺形からスタートしたが、三角形からスタートすると、また違った味わいの問題になるかも。いきなり以前書いたこちらの鳩目返しの内容ではちょっと取っつきにくいかもしれないので、今回のシリーズの後に前回の内容を持ってくると考えやすいかもしれない。

またもや毎度お世話になっているＧ先生からの出題。

トランプ５２枚を揃えて手に持つ。そのカードの一番上の１枚を捨てて次の１枚を残りのカードの一番下にもってくる、という作業を繰り返す。このとき、最後まで残っているのは最初の並びの上から何番目のカードか？

たとえば５枚のカード�@�A�B�C�Dでその操作を行うと、�@�B�D�C�Aの順に捨てられるので、答えは２番目ということになる。６枚のカードなら４番目だ。この問題は「継子立て（ままこだて）の問題」と言われる問題の変形だと思ったので検索してみると、「ヨセフスの問題」とも言われるようだ。実際にトランプでやってみれば答えはすぐに出るのだが、もっと違う枚数のカードだったらどうなるだろうか？

52枚のカードを上から１枚捨てて、次の１枚を一番下に、次の１枚を捨てて、次の１枚は下に・・・ということを繰り返すとき、最後に捨てるカードは最初の並びで上から何番目か？という問題。やってみれば分かると思うのだが、40枚目だ。これを一般化してｎ枚のカードでやってみたら・・・ということも面白いのだが、ｎの式で表すにはちょっとスッキリいかない（ので、ここでは書かない）。

ところでこのような一定手続きの操作なら、延々と繰り返していけば、いつかは最初の並びに戻るはずではないか、と思った。たとえば5枚のカード�@�A�B�C�Dでやってみると、

�@�A�B�C�D→�@�B�D�C�A→�@�D�A�C�B→�@�A�B�C�D

と、３回の操作で元の並びに戻る。これを周期３ということにする。カードが増えれば、当然周期も増えるだろうと思っていたのだが、意外なことにそうでもないのだ。たとえば10枚のカードなら周期は９なのだが、11枚のカードなら

�@�A�B�C�D�E�F�G�H�I�J
↓
�@�B�D�F�H�J�C�G�A�I�E
↓
�@�D�H�C�A�E�F�G�B�I�J
↓
�@�H�A�F�B�J�C�G�D�I�E
↓
�@�A�B�C�D�E�F�G�H�I�J

と、周期はたったの４なのだ。で、12枚のカードなら周期28と跳ね上がる。この周期を調べていくのも面白い（ので、調べた結果はまた次回）。

トランプ継子立てのつづき。前回提起した継子立てシャッフルの周期を調べてみた。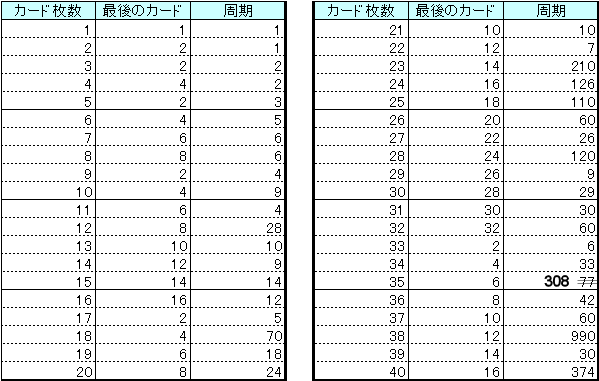

Ｃ言語でプログラムして、２回目、３回目・・・とシャッフルしたものを目視で確認したため、プログラムミスの可能性があり、目視での確認時の見間違いの可能性もあり、ちょっと信憑性の薄いデータです。何かミスがありましたらご指摘いただけるとありがたく思います。一応、Ｃ言語で作ったexeファイルをアップしときます（mamako.exe）。

ちなみにトランプの枚数５２枚だと周期は６４４。最初は実際にやろうとして３回目くらいですぐに断念したのだが、良い判断だった。４４枚だと１０００を超える周期になってしまって（たぶん）、そのあたりで調べるのを断念した。周期は大きくなる一方かと思うと、６５枚ではなんと周期７。法則をここしばらく考えてるんですが・・・。うーーーん、ひらめかない。年末というのに気持ち悪い。年越し迷宮入りとなってしまうのか？？？（つづかない）

先日の表に間違いがありましたので訂正します。３５枚の時の周期が３０８でした。すみません、そそっかしいですね。表の画像も訂正しました。

やはり目視確認には限界があるので、プログラムでチェックすることにした。最初はプログラムを考える方が面倒くさいと思っていたのだが、実際にやってみると最初からこうすればよかったなぁと反省した。目視による確認の方がよっぽど面倒くさいし、不正確だ。今まではとにかく紙と鉛筆で試行錯誤するしかなかったのだが、プログラミングを勉強し始めてから選択肢が広がったことがとても嬉しい。それで、ついでにカード１００枚までの周期表をあらためて掲載します。今度は間違いはないはずだ(と思う)。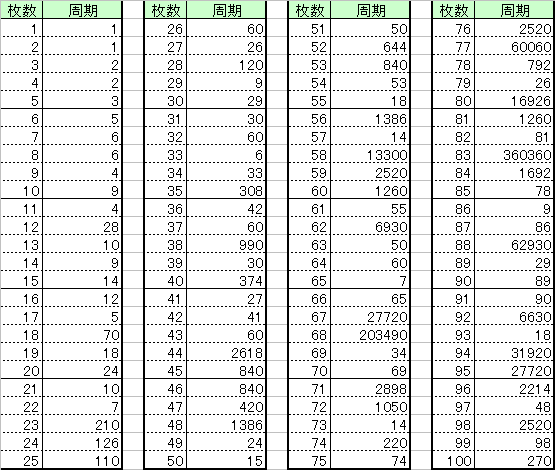

ちょっと気づいたのは、カードが5枚で周期３、9枚で周期４、17枚で周期５、33枚で周期６、65枚で周期７だから、129枚なら周期８、257枚で周期９、513枚で周期１０、1025枚なら周期１１・・・のはずだと思ってプログラムでチェックすると、その通りだった(プログラムはこちらmamako2.exe。前回のものではチェックできないので改善した。）。でも分かったのはそれくらいで、進展がない。
もうこのまま年を越そうと思います。それでは、よいお年をお迎えください。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---