大学のプログラム演習ではWindowsではなくLinuxだ。操作はかなり似通ってはいるものの、私はこれまでLinuxを扱ったことはほとんどなかったので、戸惑うことが多い。職場ではWindows一辺倒なので、Linuxについてあまり考えたことがなかったのだが、せっかくの機会なのでちょっと勉強してみようかと思っている。でも自分のパソコンをLinuxに変更したりデュアルブートにするのは危険な匂いがするし、大学の演習室に入り浸るのも気が引けるなぁ、と思っていたところに、書店でこんな雑誌を見つけた。

「これならできるLinux超入門」です。これまでのリナックス入門書と違うのは、付属のDVDに「KNOPPIX」というリナックスが収録されていることだ。KNOPPIXというのは、DVDをコンピュータにセットして再起動するとこのDVDから起動して、リナックスの環境でコンピュータを扱えるというものだ。これならコンピュータのハードディスクに影響を与えることはないし、私のように「ちょっとやってみようかな」という初心者でも安心してリナックスを体験できる。いやいや、「体験できる」というだけでなく、中にはOpenOffice.orgやGIMPなども入っていて、十分に実用的だ。DVDなので起動するたびに設定をし直さなければならないなと思ったのだが、USBメモリを併用することである程度記憶してくれるようだ。時々使ってみようと思う。

ここ数日、雨がすごい。梅雨時だしちょっと前までは水不足と言っていたから、これは喜ばしいことかもしれない。ただ地域によっては洪水のようになったり、土砂災害が起きたりして大変な状況もあるかもしれない。私の住んでいる地域ではそのような危険な状況ではないのだが、私の住んでいるアパートでは先週の水曜日に危険な状況がおとずれた。

その日の朝、外は豪雨だったのだが台風とは違って風はなかったし、子どもも登校するのに問題はなかった。で、いつものように朝ごはんを食べながらボンヤリと外を見ていると、ベランダの柱に何やら黒い物がブランブランしている。一見、テレビアンテナのコードかな？と思えるような細長いものだ。さらによく見ると柱に巻きつきながら、上の階のベランダへと登っているようだ。そう、これはヘビだ。「ヘビだー！」と私が言うと、妻も子どもも「どこどこ？」と、ベランダを覗いた。ヘビはその時すでに体の下半分くらいしか見えなくなっていたのだが、ニョロニョロと登っていく姿は確認できた。うちは４階建てアパートの２階なのだが、これはどうしたものか。箒などで下に落とせばよかったのだろうけれど、すでに時遅し。３階へと登って行って、姿が見えなくなった。急いで３階の方に電話して、「今、ベランダの柱づたいにヘビが登って行きました。結構大きなヘビなんで、お気をつけください！」と伝えたのだが・・・。３階の方からすると「２階でなんとかしてくださいヨ」という気持ちだったかもしれないが、どうにもできなかったのだから仕方がない。その後、長男が登校するときに外からベランダを見たら、３階の隣の部屋に向かって進んでいたそうだ。で、その後どうなったかは知らない。

おそらくそのヘビ（子どもがニョロちゃんと名付けた）は、この大雨を避けるために本来なら木に登ったりするところを「とにかく上に行かなければ」という気持ちでベランダの柱をよじ登ったのだろうか。何にしても、その後どうなったかわからないという状況が気味が悪い。蒸し暑い中でも、おちおち窓を開けて寝られない。もう１０年以上このアパートに住んでいるのだが、これまでも気付かなかっただけでこういうことってあり得たことなのですねぇ。ということは、もうすでに部屋のどこかにニョロちゃんがひそんでいるかも。・・・あなたの部屋は大丈夫ですか？（うちは大丈夫じゃないかも）

ちょっと考えるところがあって正２０面体の図を描いてみた。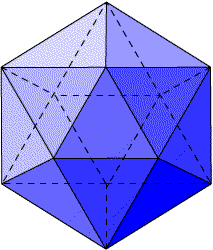

うーん、今のところは描いてみただけ。

大学では正多面体などの幾何学立体をＣＧで表現したいという目的で、現在はプログラミングの基礎を学んでいる。６月までにＣ言語の教科書を終わらせたので、７月からはＪａｖaの勉強を始めたところだ。具体的に何かを作る、という段階はまだまだ遥か遠い話なのだが、多面体を構造化するためには多面体の基本的な性質を探っておかなければならない。ということで、とりあえず多面体を座標軸上に置くことを考えることにした。

座標に置くとなると、多面体の中心を原点に置くというのが普通の考えだと思う。ここで言う多面体の中心とは、多面体の外接球の中心、ということにします。じゃあ、その中心から各頂点に引いた外接球の半径同士がなす角（中心角と呼ぶことにする）はどうなっているのだろうか。言葉で書いても分かりにくいので、正８面体で図に示します。（下図も分かりにくいかもしれませんが・・・）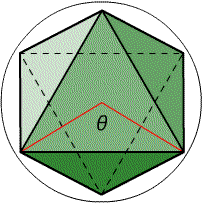

正８面体の場合は中心角θ＝９０°となることは、図を見ればすぐに分かった。では、正４面体や正６面体ならどうだろうか？（つづく）

正４面体の中心角を求めたい。この正４面体の重心（頂点から対面へ引いた垂線を３：１に内分する点）が球の中心となるので、それからベクトルなり三角比なりを使って求められるのだが、今回は別のアプローチを試みる。そのために、多面体の「双対」について説明が必要なのだが、ウィキペディアでご覧ください（手抜き御免）。要するに、ある多面体の各面の中心（重心）を頂点として結んだときにできる多面体を「双対多面体」というらしい。だから、正４面体の双対はまた正４面体になる(下図左)。

ということは、中心角をθ、隣り合う２面がなす角をαとすれば、θ＝180°−αということになる（上右図）。だから、隣り合う２面のなす角αを求めることにする。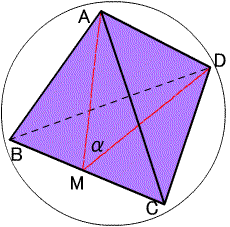

上図により余弦定理から cosα＝1/3 ということで、cosθ＝cos(180°−α)＝−cosα＝−1/3 となる。これをもとに関数電卓によると、θ＝109.47122063･･･のようです。ということは、立方体の場合はどうなるのか。（つづく）

立方体の中心角を探るために、立方体の双対多面体を調べる必要がある。で、したの画像をご覧いただくとわかるように、立方体と正８面体とは互いに双対の関係にある。

ということは、立方体の中心角θを求めるためには正８面体の面のなす角αを求めればよいことになる。そう言えば逆の関係で考えると、立方体の面のなす角が９０度だから正８面体の中心角が１８０度−９０度＝９０度ということで、辻褄があう。さて、正８面体の面のなす角について。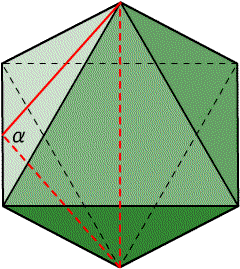

上図のようなイメージで、面のなす角αを求めたい。立体だとイメージがわきにくいので、これを横に倒して真正面から見て平面的にとらえることにする。

ちょっとわかりにくいのですが、左の動いているやつは正８面体を倒して真正面から見たものが回転していると思ってください。こう見ると右図のような三角比になって、余弦定理からcosα＝−1/3 ということがわかる。したがって、立方体の中心角θについて cosθ＝cos(180°−α)＝1/3 なので、θ＝70.5287793655･･･となります。さて、つぎは正１２面体と正２０面体なのだが・・・。（つづく）

正12面体の中心角θを求めるために、その双対多面体である正20面体の面のなす角αを求めればよい。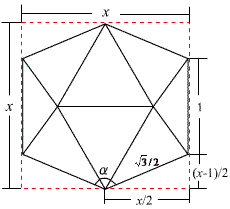

正20面体を面のなす角αが正しく見えるように置くと上図のようになる。図からとなるから、cosα＝なので、cosθ＝より、正12面体の中心角はθ＝41.8103･･･となります。次回は正20面体の中心角を求めます。

正20面体と正12面体は互いに双対の関係にあるので、正20面体の中心角θを求めるために正12面体の面のなす角αを求めることにする。前回の正12面体のときと同じような方法で考えた。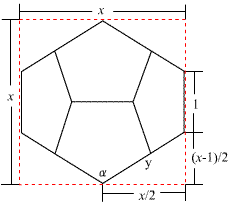

図のyの部分がという、ちょっと面倒な数字になります。それでも強引に計算していくと、cosα＝と、思ったよりも簡単な数字になります。ということは、もっと簡単なアプローチがあるのでしょうね。まあ、とにかくcosθ＝となって、θ＝63.4349488･･･となります。実はこの答えに至るまでに大きな勘違いをしていたようなので、次回はそのことについて。

まず7月10日に載せた画像を再掲します。

これはドロー系のソフトで描いたイラストですが、本来見えている姿を優先せずに、私が描きやすい描き方で「とにかく正20面体に見えればいいや」ということで描いたものです。だからよく見ると、真ん中の正三角形はいいとしてその周辺の三角形も正三角形になっています。ところが実際に正20面体をこの角度から見ると、周辺の正三角形には角度がついているから少し歪んだ三角形に見えるはずです。そこのところをごまかしていました（スミマセン）。で、改めて描き直したイラストをご覧ください。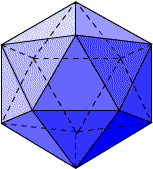

こちらの方がより実際に近い形かと思います。が、正確に計算して描いたわけではないので、これも少し怪しいところです。
さて、ところでこういうものを描いていると、正20面体のこの角度からのシルエット（正射影）は正六角形になるのだろうな、という思い込みを持っていました。まあ、上の図はごまかして描いているので正六角形になるのですが、下の図でもなんとなく正六角形なんだろうなと。何しろ正20面体は対称性の高い奇麗な立体ですから。

ところが、その前提で中心角を計算すると、微妙に違う値になるんです。cosθ＝となって、θ＝64.7194468･･･になります。この値はθ＝63.4349488･･･とは微妙に異なります。で、インターネットなどで調べると後者が正しいようです。ということは、この正20面体のシルエットは正六角形ではないんですねぇ。今頃になって初めて気付きました。いやはや、お恥ずかしい話です。

先日、「正２０面体のシルエットは正６角形にならない」と書いたところ、紙折ってる場合だろ！のkawachoさんからご指摘をいただいて再検討したところ、大変な勘違いをしていたことに気付きました。kawachoさん、ありがとうございました。２日間野ざらしにしていたので、その間に見て鵜呑みにされた方がいないことを祈ります。いやはや、恥ずかしい限りですが、恥かきついでにどうしてそんな勘違いをしてしまったのか、ちょっと説明したいと思います。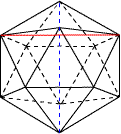

正２０面体の一辺の長さを１とします。すると、上図の赤い対角線の長さはになります（上から見たときに一辺が１の正５角形の対角線だから）。で、仮にこの図が正６角形ならば、青い点線の対角線の長さがとなって、正２０面体の外接球の半径がその半分となるので、そこからcosθを計算して失敗しました。さて、この考えのどこが間違っていたのでしょうか。

昨日、とんだ大間違いの更新作業を終え、ひとり寂しく敗北感と劣等感と自己嫌悪に打ちひしがれながらメールチェックをしたところ、見慣れないアドレスから一通のメールが届いていました。ななな、何とJuno's WorldのYananoseさんご本人からです。まさに椅子から転げ落ちそうな勢いで驚きました。この辺りでも書きましたが、ずっと以前にJuno's Spinnerという幾何学おもちゃを購入して以来、Yananoseさんのことは一方的に存じ上げており、雲の上の憧れの存在の方です。その方から直々にメールを戴けるとは！！しかも大変緻密な多面体データをいただきました。ありがとうございます。こんな嬉しいことがあるのなら、何度でも大間違いをしてみせる自信があります。いやいや、失敗を恐れずにチャレンジしろ！と激励された気持になりました。本当にありがとうございました。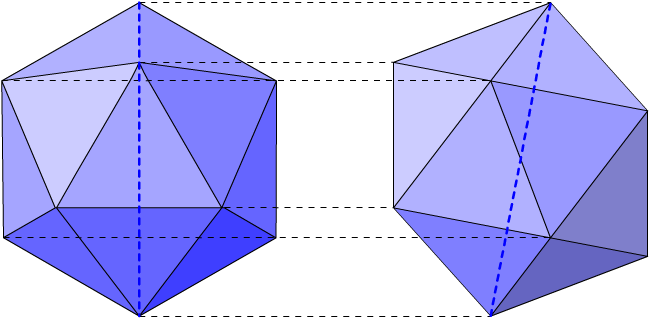

勘違いの原因は青い点線が鉛直方向にまっすぐだと思い込んでいたためでした。左画像を真横から見たものが右画像です。こうすると明らかに青い点線は傾いていることがわかります。これは確かに外接球の直径ではあるのですが、正射影したものは同じ長さだとは言えませんね。ああ、恥ずかしい。しかし怪我の功名というか、救う神ありですね。悪いことあれば良いこともある。こういうのをカルマの法則というのでしょうか。ということは今度は「良いことあれば悪いことあり」なのか？

世の中の小中高校はもう夏休みに入ったところだろうか。我が家の小中学生は既にドップリと夏休みモードに入って、自由な時間を満喫している様子。高校３年生を担任していた昨年の今頃を考えると、まだまだ補習の真っただ中で、授業準備や調査書の作成などに忙しい毎日だった。８月９日まで補習で、その後は家庭訪問、合間を縫ってサッカー部の練習や試合など、今思えば殺人的なスケジュールだったように思う。よくあれだけの内容をこの暑い中やれたものだなあと、我ながら感心する。あの頃は若かったなぁ、、、とか言って、１年しか違わないのだけれど。

今年は大学では８月２日に前期最後の試験があって、その後夏休みに入る。と言っても、私の場合は普通の学生と違って講義が無いからと言ってもなんら研究に支障はないので、基本的には研究室でお勉強することになる。が、例年の夏休みとは違って家族サービスをするくらいの自由な時間は取れそうだ。来年以降も夏休みだからと言って家族サービスをできる保証はないので、今年が唯一のチャンスだ。ということで、８月になってから旅行を企画している。また旅行後に道中の記録をここに書きたいと思います。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---