今日は卒業式だ。わがクラスの４９名もいよいよ卒業である。この一年はとても長かったような気がする。それだけ内容が濃い一年だった、、、と解釈しよう。
ところでこの時期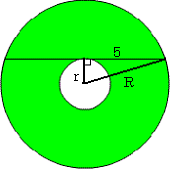の卒業式はイマイチ感慨に浸れない。国公立大学の前期試験を受験した直後で結果待ちの状態だし、後期試験に向けてまだまだ準備を進めなければならないからだ。実際、わがクラスの生徒たちも卒業式が終わった午後から、後期試験の面接練習だとか、小論文対策だとか、まだまだ大変なのだ。卒業式だからといって泣いている場合ではないのである。合格が決まってから、ともに喜び合いたい。

さて、一昨日の問題。

図のように外側の円の半径をＲ、内側の円の半径をｒとすると、三平方の定理からＲ²−ｒ²＝５²である。
ところで、緑のリングの面積は、πＲ²−πｒ²なので、πでくくって、π（Ｒ²−ｒ²）であるから、２５πということになる。この答えはＲとかｒには関係ないので、一昨日の２つの図形はどちらとも同面積の２５πなのである。

答えがＲやｒに関係ないのであれば、内側の円の半径ｒを究極まで小さくして「点」にしてしまったらどうだろうか。線分は外側の円の直径になり、求める面積は外側の円の面積となる。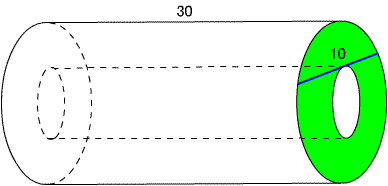

ということは、上図のような長さ３０の管があって断面が前回のようなリング状だったら、この管の体積（中の空洞は除く）はいくらでしょうか？

３月１日は卒業式だった。三年間ともに学んだ仲間たちと別れるのは少し寂しいものだが、それぞれ次に待っている新しい生活に期待を寄せる表情がうかがえて、とても頼もしく感じた。私も不覚にも（ほんの少しだけ）ウルウルきてしまった。
最後のホームルームが終わった後、毎年恒例のサッカー部の記念品贈呈式を行なった。今年の３年生は６人と少なかったが、それだけに最後の高校総体までよく頑張ったと言える。マスコットボール（流行のチャンピオンズリーグ様式の物。メンタマつながりのおまわりさんみたいなデザイン）に後輩が寄せ書きをして、一人ひとりに手渡した。すると昨年に続いて卒業生側から私に「３年間ありがとうございました。」と、記念品をくれた。

プロフェッサーキューブである。さすがにコヤツら、私のツボをよく知っている。６人が６面に寄せ書きをしてくれている。そのお陰で難しさが増しているのではないかと思う。

さて、前回のチューブの体積は（底面積）×（高さ）だから、25π×30＝750πですよね。では、次の体積はどうでしょうか？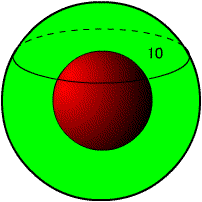

大きな球の中に、中心が同じである小さい赤い球がある。その赤い球と大きい球に図のように接する円板の面積が１０のとき、緑の部分（大きい球と小さい球の間の部分）の体積はいくらでしょうか。球の半径には関係ないのでしょうか。

アクセスカウンターが３万を超えたようです。いつも訪問していただいてありがとうございます。

ところで日曜は親子サッカー大会だった。子どもが所属するサッカーチームで、６年生を送る会とともに毎年行なうイベントである。私も昨年に引き続き出場した。昨年よりも天気がよく暖かかったものの風が強くて、花粉症の私はマスクをしてサッカーをした。ちょうどガンバ大阪からザルツブルクへ移籍した宮本選手がアイマスクをしていたみたいだとイメージしていただけると有難い。花粉症マスクとアイマスクの違いは、この際取るに足りない微々たる違いだ。ついでに私のプレーぶりも宮本選手をイメージしていただきたいと願う。

昨年と大きく違う点は、私が準備不足ということだ。つまり昨年よりも運動不足なのだ。私は曲がりなりにも高校のサッカー部の顧問をしているので、昨年のこの時期は、普段から高校サッカーのきびしい練習中に行なった球拾いや草むしりなどで十分に鍛えていたのだ。ところが今年は３年生のクラス担任だったため、ここ半年くらいは部の練習をほったらかしにしていたものだから、十分な鍛錬ができなかった。もともとウルトラマン並みの持久力（３分間しかもたない、ということ）だったのに、今年はほんのワンプレーにかけるしかない。問題はその貴重なワンプレーをどの場面で発揮するか、ということである。キックオフ直後に１０ｍくらいダッシュして力尽きたら、その後の延々と続くゲーム時間は悲惨な状況になる。よく考えて力の出しどころを見極めなければならない。

ということを色々と考えていると、監督さんが、「ウォーミングアップをしましょう」という。まずは柔軟体操から。次に軽くランニング。そして、最後に１０ｍのダッシュ。・・・この後はご想像におまかせしたいと思う。とにかく昨日・今日は階段の昇り降りがつらい。

さて、前回の問題。

大きな球の中に、中心が同じである小さい赤い球がある。その赤い球と大きい球に図のように接する円板の面積が１０のとき、緑の部分（大きい球と小さい球の間の部分）の体積はいくらでしょうか。球の半径には関係ないのでしょうか。・・・という問題でした。
が、この体積は球の半径に関係ありで、これだけの条件ではズバリの答えは出せないようです。内側の球の半径を大きくすればするほど、円板の面積を１０に保つために外側の面積も大きくなり、その隙間は狭くはなっていくのですが体積は増加していき、一定ではありません。少し意地悪問題でした。

次回、もう一回だけ同心円に関する問題を出題して、この話題を終わりにしたいと思います。

昨日は高校入試だった。普段にも増して間違いの許されない仕事だし、さまざまなアクシデントを想定しなければならないので、緊張した一日だった。そのアクシデントについて何か書こうかと思ったのだが、この業務には守秘義務があって、どんな些細なことでも外部に漏らしてはいけないとのことなのでここでは書けない。（ホントはネタが無いから書けない。）精神的に疲れる一日だった。

さて、同心円の最終回。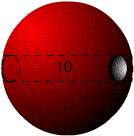

上図のように、球の中心を真っ直ぐに突き抜ける穴があいていてその長さが１０とするときに、この立体（穴があいた球）の体積はいくらでしょうか。これは下図のように球の半径が大きいとしても半径には関係ないのでしょうか。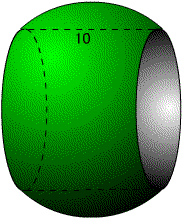

昨日まで高校入試のため、隣の高校で入学試験や採点業務などを行なった。隙間の時間にはインターネットで国公立大学前期試験の合否が続々と判明し、一喜一憂している。今のところ四喜一憂くらいの割合で、全体としては例年以上にうまくいっていると思う。わがクラスの４９名の中では大阪大に１名、九州大に３名、お茶大に１名をなど、難関大学にも無事合格して、すでに３０名以上の生徒が国公立大学に合格が決まった。東京大、京都大にも１名ずつ結果待ち（１０日が発表）の者がいるので、私は一生懸命に祈っているところだ。
一方で前期試験に不合格だった者は今日も学校に出て後期試験対策を行なう。最後の最後まで頑張り抜いて欲しいと思う。

さて、前回の穴あき球（数珠みたいなやつ）の体積の話。

これが実は同じ体積になるのだ。積分をしてみれば体積が等しいことがわかるのだが、積分を習っていなければ難しい問題だったかも。
ただ、この２つの体積が等しいことさえ分かっていれば、その体積は中学生でもわかるだろう。球や穴の半径には関係なく体積が一定ということは、穴の半径を究極まで小さくして０に近づけても体積は同じのはずだ。だから、求める体積は直径が１０の球の体積に等しい、と考えられるので、３分の５００πである。

前期最後の合格発表だった東大君と京大君、みごと合格してました。この２人、本当にすごいです。色々な意味ですごすぎです。特に私がありがたかったのは、その存在感。クラスメイトが「駄目だ、俺にはわからない」、「限界だ」と思った時に、同じクラスにこの２人がいるわけですよ。同じ授業を受けてて、弁当を見ても同じようなものを食ってる。その２人が「できる」ということは、ひょっとして自分にもできるんじゃないかと。何かそういう目に見えない効果がジンワリとあったような気がします。いやはや、ホントにおめでとう！
２人に限らず私のクラスから大学に合格した者達に言いたい。みんなが合格できたのは多くの先生方に支えられたのと同時に、私が極力関わらなかったお陰である。クラス担任でありながら極力関わらない、というのは至難の業なのだ。私が深く関わっていたらこんなに上手く合格できるはずがない。言い換えれば、私のお陰で合格できたようなものである。早く立派になって、私が落ちぶれた頃に恩返しをして欲しいと思う。お礼参りは遠慮したい。

ところで、今日が国公立大学の後期試験。前期試験で打ちのめされたにもかかわらず、最後の最後まで頑張りぬくこの姿勢を大学側には買って欲しい。まあ、定員枠があるので全員入れるなんてことは無理なのでしょうけど。しかし私の立場からすると、大半の高校３年生が進路が決まってほっとしている中を、こいつらは今の今まで頑張り続けているのだから、前期試験よりも一層「合格して欲しい」と願う気持ちが強い。結果は３月２１日くらいに発表される。本当に最後まで気が抜けない（祈るのに忙しいのだ）。

先日、ベネッセコーポレーションの方からメールをいただいた。ベネッセと言えば進研模試だ。私が生徒によく言っている「進研模試は真剣に受けなさい」というハイブローなギャグに対する抗議だろうか。もしかしてこのギャグには著作権が存在するのだろうか。そう言えばこのギャグを言った後の生徒の反応はどこか戸惑ったような感じで、私は孤高の雰囲気を味わっていたのを思い出した。そんなことを思いながらよく読んでみると、「公立中高一貫ネット」という、公立中高一貫校進学を希望している小学生の保護者向けのサイトを運営している方のようだ。実はうちの長男は小６なので、勧誘のメールか？とも思ったのだが、さらによく読むと、そのサイトから発信するメールマガジンでカライドサイクルのページを紹介してもよいか、という問い合わせだった。ベネッセさんには模擬試験で私の生徒たちも大変お世話になっている上に、著作権侵害までしているかも知れないのだ。この問い合わせを断ったら、「訴えますよ」と言われかねない。ここはひとつ穏便にことを済ませたい。私のページをメールマガジンで紹介されるくらい、少々恥をかくくらいのことだ。
ベネッセさんには「大変光栄に思います。どうぞよろしくお願いします。（そのかわり訴えないでください）」と返信しておいた。カッコ内はもちろん書いていない。ベネッセの方なら行間を読むくらいのことはできるだろうと思う。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---