今日は９月３日の振り替え休日で時間があったので、朝っぱらから工作をした。昨日まで数日間は調査書作成のため４時間睡眠が続いていたので今日はゆっくりと眠るつもりだったが、早起きが癖になってしまって５時くらいに目が覚めたのだ。

いつかこのあたりで正四面体を分割して正八面体のハトメ返しにするものを作ったが、今度は正八面体を８個に分割した立体をハトメ返しにしたらどうなるのだろうか？と思ったのだ。

右の図の立体を８個作ってつなげてみた。

組み立てた図はまた次回。

土曜日は散髪屋で髪を切ってもらった。散髪をした後は自分は気持ちが良いのだが、周囲からの反応は良くない。子どもがまだ赤ん坊の時には泣かれたこともあった。生徒からは「先生、何で切ったん？（やめておけばよかったのに）」とか、必死で笑いをこらえている者とか、目を合わそうとしなかったりとか。
昨日も生徒から、散髪代金は幾らか、と聞かれたので正直に３千円だと答えたら、「それじゃあ僕らと同じですよ。損をしたとは思いませんか？（僕らの髪の毛を切るよりも手間も時間も量も少ないはずなのに）」という容赦ない質問をぶつけてくる者もいるくらいだ。「私の髪の毛は君らのものとは中身が違うのだ。なにより希少価値が高い。」と答えると、「なるほど」と納得したようだった。なかなか理解力のある頭のよい生徒である。

さて、先日の８面体を分割した立体の続き。

黄色の面を表にして組み立てると正八面体になる。内側は隙間がない、つまり単連結である。そもそもの発端が正八面体を分割したのだから、当たり前である。では、青い面を表にして組み立てるとどうなるのか？

これはなんという立体なのだろうか？イガイガ、というかデコボコとした立体ができた。こちらは単連結ではなくて内側に正八面体の隙間ができる。

青い面を表にする組み立て方の別バージョン。

立方体が２つつながった形の直方体ができた。立方体の中の空間は正四面体になっている。

立方体の中に正四面体があり、しかし元々は正八面体だったのだから、面白い関係だと思う。

ｘ²やｘ³のｘに大きな値を代入するとそれはさらに大きな値になるのだが、２^xのｘに大きな値を代入しても相当に大きな値になる。では、ｘ²と２^xではどちらがより大きな値になるのか、、、という問題はすぐにお分かりになると思う。ｘの値が同じなら、２^xの方が圧倒的に大きな値になる。これを実感させるために、「新聞紙を100回折りたたんだら、どれくらいの厚さになると思うか？」というような質問をすることがある。これはよく聞く話なので、「知ってるよ」という生徒も結構いる。

数年前にある先生から聞いた、その種の例え話。
「公衆電話で電話をかけようと思ったが１０円玉がなかったので友人に貸してくれないかと頼んだところ、『１分１％の複利だ』と言って快く貸してくれた。その次の日のちょうど同じ時刻に返すとき、いくら返せばよいだろうか」
という問題である。さて、いくらでしょう？

「１分１％の複利で１０円を借りた。ちょうど１日後にいくら返せばよいか？」という問題の答えは「１６７０万円」になる。計算式は10×1.01¹⁴⁴⁰

この問題の面白いところは、全ての数字が比較的とても小さいのに、結果が予想以上に大きくなる点。たった１０円をほんの１日借りただけ、しかも１％の利子というのも低金利なのにどうしてこんなことになるのか。からくりは「１分１％」の１分にある。刻み幅が小さいということは利子を加算する頻度が高いということで、この問題では1440乗という大きな指数となる。指数の部分が大きくなると、元々の数字が小さいものであっても雪だるま式に大きくなる例である。

この問題は生徒にとっても身近な問題なので興味を引くようである。数字も現実味があって想像できる範囲内のものだ。何よりも高校卒業後に闇金融などに騙されないように釘を刺す効果はあるのではないかと思う。心配なのは、騙す側に回らなければよいが、ということである。

こちらのブログで紹介されていた、星型１２面体を作ってみた。型紙も掲載してくれているのでありがたいです。

型紙を切って組み立てると上写真のように２つに分かれてできあがる。これをつなげて星型１２面体ができる。

凸多面体の場合は山折ばかりだったが、これは型紙から組み立てるときに山折と谷折があるので気をつけないといけない。その点、この型紙では親切に点線と実線でわかり易く示してくれているのでありがたい。ただ、２つを組み合わせるときに最後の最後は糊付けができないが、こんなときは皆さんどうしているのでしょうか？人生、山折り谷折り、ということか。

先日作った星型12面体の写真を掲載したところ、メールをいただきました。ありがとうございます。その中に「紙の上に正１０角形の頂点が与えられると定規だけを使ってこの立体の正射影図を描くことができます。」とあったので、実際にやってみた。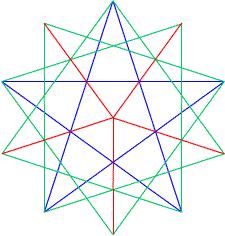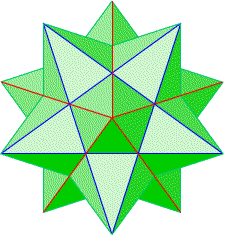

ホント！うまくできました。一番上は正１０角形の頂点を結んでみたところ。真ん中は色をつけて陰影をつけてみたところ。最後に線を抜いたら我ながら結構きれいにできて嬉しかったです。

先日の星型12面体の作図の続き。

GIF画像だとなんだかツブツブになってしまったので、改めてJPG画像で掲載。右は手近にあった立体を模写したもの。あんまりうまくいかなかったようですな。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---