あそびをせんとやさんにコメントをいただきました。補足をしていただき恐縮しています。ありがとうございます。小学校６年生のときの担任の先生は素晴らしい方ですね。何年も前の授業の一こまを覚えていらっしゃったhaseさんの感性も素晴らしいと思いますが、その感性を掘り起こした担任の先生にも敬服します。私もこうありたいものだと思うばかりで、日々つまらない授業を積み重ねております。特に大学受験のための数学の授業というものはトレーニングの要素が強くて、生徒もつらいと思いますがそのような過程を乗り越えて分かる面白さもあるのだと（自分にも）言い聞かせながら・・・。

もちろん昨日書いた「正方形の２辺の長さと対角線の長さは等しい」というようなものは間違いです。簡単な解説を下に示します。

まあそりゃ、冷静に考えればそうなんでしょうけど、それならなぜ昨日のような錯覚を起こしたのでしょうか？

正方形の刻みを多くしていくと、ジグザグにすすむ赤線は段々と対角線みたいになっていくように見えます。ところがこれは、「なんとなく」、「遠くから見ると」、「ぼやかしてみると」みたいにごまかしが入ると思うのです。きめ細かに刻んだ時にはそれ相応のきめ細かさで詳細に見なければならない、ということではないでしょうか。

道の幅が０ではないとすると、話は変わってきます。下に極端な図を示します。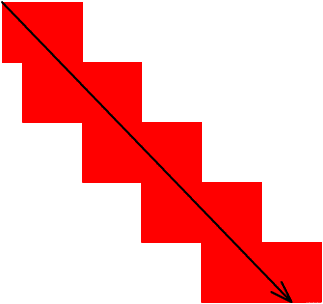

この図のように極端でなくても少しでも幅があれば斜めに進んでいけるため、赤線の方が近いと言えます。このように実際の道であれば中を突っ切って進む道のほうが近道であると言えるのですが、曲がる回数が多い赤線よりも曲がる回数が１回である外回りの方が時間的には速い場合もあるかと思います。

５月２６日に紹介した「穴あき正十二面体」ですが、紙を裏返しで作ったりセロテープだらけだったりで不本意だったので、もう一つ作りました。

前回のものよりも２回りくらい小さいので、閉じた時の締りが甘くていまひとつの出来具合です。しかしもう一個作り直す元気も時間もなく、どうせ「穴あき」ということだし、もういいかなという感じです。

こちらのブログで回文数についての算数オリンピック問題を紹介されているのを見て、そういえば遥か昔、回文にこったことがあるなあと思い出しました。回文というのは上から読んでも下から読んでも同じ文のことです。当時のお気に入りをいくつか。

• 電話あれこれ、あわんで


• Ｖ宣言、西武


• ヘアリキッドけつにつけ、ドッキリアヘ

「回文」で検索してみるとやっぱりあるんですね。回文の部屋はすごい量の回文を紹介されています。全部見たわけではないのですが、この中の私のお気に入りは、

• 内科医、中に何かないかいな


• 和久井映見と俺と森本レオと三重行くわ

状況がイメージされやすいものが面白いですね。

昨夏、鹿児島県にお邪魔したときに同志の先生から教わった「落ちていくリング」をご紹介します。まずは動画をご覧ください。

落ちていくリングの動画（262KB）

確かにつながっているはずなのに、一番上のリングが一番下までコロコロと落ちていきます。

鹿児島では教員の学習会のようなものに参加させていただいて、私も手持ちネタをいくつか紹介しました。本当は私が講師という立場だったのに逆に色々とよい刺激をいただいて、その上この「落ちていくリング」までいただきました。そのときお世話になった佐藤先生をはじめ参加された先生方、ありがとうございました。リングをいただいた晩、早速100円ショップで買ったカードリングを20個ほどつなげてみたのですが、かなり注意して繋いでいかないとうまくいきませんでした。今回この場で紹介するために新たに繋いでみたのですが、いまだに完成物を見ながらでないとうまく繋げきれないという情けない状況でした。

昨日のあそびをせんとやさんの三方八面体(?)の問題ですが、ようやく私もこういう問題にこなれてきたのか、イメージすることができました。というか、以前に作ったことがあるからイメージできたのですが・・・。こういう話題に触れると、また作りたくなってきました。早速作ってみようと思います。

いよいよ始まりましたね。ドイツＷ杯。まだ始まったばかりなのに巷であんまり騒ぐものだから、その反動でそれを抑えようとするような向きも私の周りでは感じられます。高校３年生としてはＷ杯どころではなく勉強しろ、というところでしょうか。４年前の日韓大会の時はゴールデンタイムに放映されていた試合が、今年は深夜だとか早朝とかになるわけですから、生活時間を乱されることは必至です。３年生のクラス担任であり、サッカー部の顧問でもある私にとっては非常に苦しいところです。サッカー部の部員には常日頃から「サッカーを言い訳の材料にするな」というようなことを言ってはいるので、今回も「見てもいいけどそれを理由に勉強をサボってはいけない」と言っていますし、部員はきっとこんな時こそ頑張ると思うのですけども、問題はＷ杯期間限定の「にわかサッカーファン」の生徒たちです。とにかく生活の乱れから体調を崩したりしないようにしてもらいたいものです。

私が子どもの頃、初めてＷ杯をテレビで見たのは７８年のアルゼンチン大会でした。うちは父が電気屋をやっていましたので（今でもやってるのですが）、当時はまだ珍しかったＶＨＳの家庭用ビデオがすでに我が家にはあっったので、そのＷ杯総集編のビデオなどを友達が見に来たことを覚えています。その大会はアルゼンチンが優勝したのですが、まだマラドーナは１７歳くらいで代表には選ばれていなかった頃です。ケンペスという選手が得点王に輝いて時の人となりましたが、私はアルディレス選手がお気に入りでした。アルディレスはその後清水エスパレスなどＪリーグの監督にもなりましたのでご存知の方も多いかと思います。当時のアルゼンチン代表は背番号をアルファベット順につけていて、当時でも普通１番はゴールキーパーがつける番号なのに、アルディレス選手が１番をつけていたように覚えています。

Ｗ杯でメディアも様々な特集番組を組んでいて、テレビの見所も満載です。最近ではＮＨＫスペシャル「“プレス”を磨け」が秀逸でした。ともするとゴールシーンに偏りがちな特集番組の中で、地味ながらも組織的なディフェンスに目を向けており（しかもその「プレス」こそがここ数年の世界的な流行なのですが）、もう十年前とは格段のレベルの違いがこういうところでも感じられます。ビデオに録画したので、先日雨の日に部員にはその番組を見せました。この番組を見た後にＷ杯の試合を見れば、ゴール前以外の攻防も興味を持って見られるのではないかと思います。

先日のあそびをせんとやさんの三方八面体の話題、「正八面体の表面に正四面体を合同に４分割した三角錐を貼り付けたらどうなるか？」という問題です。すでにあそびをせんとやさんで綺麗なCGを使ってわかりやすく示されていて、（つづく）ともなかったので、私もこの話題に便乗しようと思います。衝動にかられて実際に作ってみたので、写真を掲載します。

左のが正四面体を合同に４分割した三角錐です。右の写真は４つ集めて正四面体にしている途中です。これを８個作ってつなげたのが次の写真です。

これを白い方を表にして組み立てると正八面体になります。

赤い方を表にして組み立てると、菱形十二面体になります。

これらはどちらも単連結ではありません。つまり中に空洞ができます。例えば菱形十二面体（赤い方）にした時の中の空洞は正八面体になっています。ではここで問題です。正八面体（白い方）にした時の中の空洞はどのような形をしているのでしょうか？

今、朝の５時過ぎですがかなり強い地震がありました。震度５弱らしいです。少し不気味です。

赤い菱形十二面体の蓋を開けると右下のような感じです。中の空間は正八面体になっています。

では、これを裏返して白い正八面体にした時に、中はどのような隙間が空いているのでしょうか？

なんだかザクロみたいです。明日はこの隙間立体についてです。

サッカー日本代表、ストレスたまりました。自分のチームの試合を見ているようでした。

昨日の隙間立体です。

(ルート６)：(ルート６)：４の二等辺三角形を24枚でできています。最初アレキサンダースターかと思ったのですが、こちらは正面から見て正五角形ではなく正方形です。なんと言う名前の立体なのでしょうか？教えていただければ嬉しいです。
これ、先の正八面体-菱形十二面体の中に収めたかったので、少し小さめに作りました。少しだけ、と思ったのですが、かなり小さいですね。

この隙間立体、膨らませたらどうなるのでしょうか？

単連結ではない立体ハトメ返しでできる隙間立体の話題は「隙間を埋める」という点において私向きのテーマだと思って気に入っています。(今回のように隙間を埋めるには少し小さめで埋めきれていないのですが)

昨日のアレキサンダースターみたいな立体を膨らませると（へこんだ部分を膨らむ方向に折ると）どのような立体になるのでしょうか？先日のものとは別にもう少し薄い紙で作ってみました。

左が昨日の立体です。このへこんだ部分を強引に膨らむ方向に引っ張り出すと右のようなことになります。菱形十二面体になりました。実はこの説明は反対で、まず菱形十二面体を作って頂点をへこませたのです。作る際に各面の長辺に折り目をつけておくのがうまく作るコツです。

さらに実は最初の写真は同じ立体の半分ずつでした。横から撮影した写真をご覧ください。こんな半分半分のものを「アシュラ男爵みたいに・・・」と形容して通じる世代って、何歳くらいまでなんでしょうか？

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---