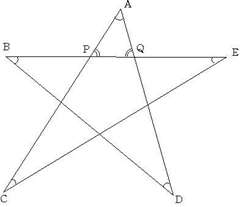三角形の外角は他の二つの内角の和に等しいので、∠P＝∠C＋∠E、∠Q＝∠B＋∠Dです。△APQにおいて∠A＋∠P＋∠Q＝180°なので、結局
∠A+∠B＋∠C＋∠D＋∠E＝180°になります。

これはよく見かける問題だと思います。では、下の図で∠A〜∠Gまでの和はそれぞれ何度でしょうか。

今日は卒業式です。でも、まだ進路が確定していない者もいて、感慨に浸ってばかりもいられません。

昨日の角度の求め方でも何とかできるかもしれませんが、なんだか図がゴチャゴチャして混乱してしまいそうです。そこで、別のアプローチをしてみます。昨日の右図で説明します。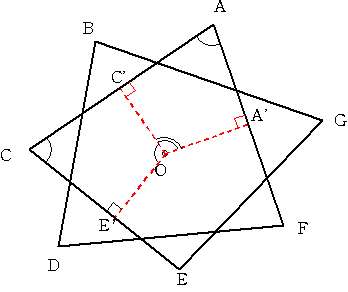

上図はグラウンドに大きく図を描いてみたとして、真ん中辺りの点Oに私がいるとします。次に友人のヒトシくんに点A'から線に沿って点Aの方向に動いてもらいます。このとき、私はヒトシくんを目で追いかけます。実際は目だけではなく体ごとヒトシくんの方向に向けてその場で回転するように追っていきます。つまり、私は最初A'の方向に体を向けているのですが、ヒトシくんが動くにつれて点A'→点A→点C'へと体の向きが変わっていくとします。
ヒトシくんがA'からC'まで動いた時に、私は∠A'OC'の角度だけ回転したことになります。四角形OA'AC'で考えれば四角形の内角の和が３６０°で、９０°を２箇所使っていることから∠A'OC'＝180°−∠Aという式が成り立ちます。同様に、ヒトシくんがC'→C→E'と進むと、私は∠C'OE'＝180°−∠Cだけ回転します。これを同様に繰り返して最初のA'にヒトシくんが戻ってきた時には、私はその場で２回転しているはずですから、720°回転したことになります。これを式で書くと、

(180°−∠A)＋(180°−∠C)＋(180°−∠E)＋(180°−∠G)＋(180°−∠B)＋(180°−∠D)＋(180°−∠F)＝720°

これを計算すると、∠Aから∠Gまでの和は540°と言うことになります。

この考え方を使うと昨日の左側の問題も、和が180°という答えが出ると思います。では、下の問題はどうでしょうか？∠A〜∠Iの大きさの和を求めてください。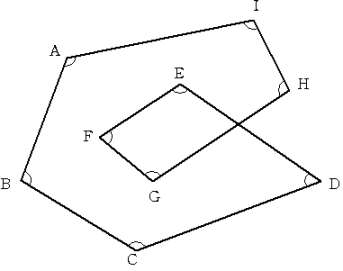

あそびをせんとやさん、いつも訪問していただいてありがとうございます。「さてどんなふうに話はまとまるのだろう」とは奇遇ですね。私も同感です。あまり後先考えず、いつもの調子でぶちまけてしまった次第です（お恥ずかしい限りです）。民主党の永田議員の心境です。こうやって時間を稼いでいる間に、何か画期的なことをひらめかないかな、と思っているのですが。。。今となっては「ぶちまけたのが国会でなくてよかった」と思うようにしています。

あそびをせんとやさんの「ppバンド多面体」、おもしろそうですね。何よりもお金がかからなそうなところが私向きのテーマです（山本さんの割り箸コースターも！制作費８０円というのもスゴイ）。こんなおもしろいものを数年前に作っておいてストックしておくあたりがすごいと思います。

さて、本題に戻って何とかしてまとめなければ！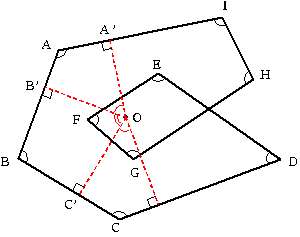

前回と同様に考えてできる問題なので、
(180°−∠A)＋(180°−∠B)＋・・・＋(180°−∠I)＝７２０°を計算して、∠Aから∠Iまでの和は900°です。

でも次のような図だったらどうでしょうか？∠Aから∠Lまでの大きさの和を求めてください。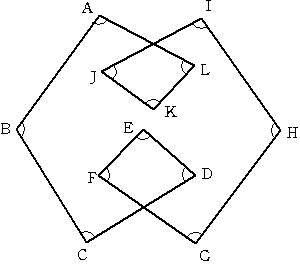

卒業式の日の話ですが、サッカー部では後輩が記念のマスコットボールに寄せ書きをして卒業する先輩に贈るのですが、なんとその後に「それじゃ、これは俺たち（卒業生）から」と言って、私にこんなものをプレゼントしてくれました。

小さい方には寄せ書きをしてくれています。本当に嬉しかったです。

昨日の朝、職場に兄から電話があり、「答えが違ってるよ」と。よく考えると１０直角を1800°としていました。持つべきものはよい兄弟ですね。ありがたいです。しかし、職場からアップロードができず、訂正できたのは昨夜９時くらいでした。その間にご覧いただいた方にはご迷惑をかけました。今後も間違いが多々あると思いますが、気軽にご指摘いただけるととても助かります。
授業中に計算間違いをした時には、「もちろん君らを試したのだ。間違いに気付かなかった人は恥ずかしいと思いなさい。」とか言ってはぐらかすときがあるのですが、ここだとそうもいきませんね。「間違い探し」の要素も合わせて、気軽に楽しんで見ていただけるとありがたいです。

昨日の２回ループの問題です。一昨日の考え方を使うとすれば、下図のように変形して２重ループにするとできます。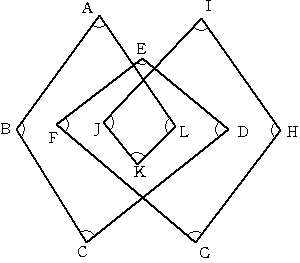

「180°×12頂点−(和)＝360°×3回転」だから、(和)は12直角で1080°になります。でもこんなに大胆に変形しても和は保たれるのか、という大きな問題が残ります。ちょっと暗算で考えようと思う分にはこの方法は有効かもしれませんが（暗算でやってるとまた間違えてしますのですが）、中・高生に説明するには無理があります。説明する時は次の図の方が良いかもしれません。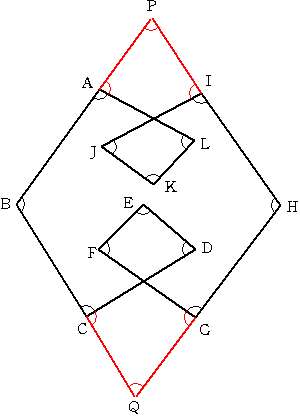

四角形PBQHの内角の和360°に、点A,C,G,Iにできる180°×4を加えて1080°です。

で、その・・・、まとめというか、落としどころというか、特に落ちはないのです。その点においてアンガールズみたいです。「ジャンカジャンカ」言いながら幕を閉じたいところです。実は苦し紛れにここで作った爪楊枝みたいに立体になると角度はどうなるのか、と思ったのですが、自由度が高すぎてどうにでもなるようです。次に考えたのが、三角形の内角の和が180°であるように四面体の各面のなす角には何らかの縛りがあるのではないか、ということです。ある２つの面のなす角が大きかったら他の面のなす角は小さくなるように思うのですが・・・。立体になると途端に難しくなります。もうちょっと考えて何か思いついたらまたここに書きたいと思います。何かヒントなどご教授いただけるととても嬉しいです。

ろくはロッパの･･･さんが、見事に落としどころを見繕ってくれました。ありがとうございます。なるほど、外角に目をつけるのですね。

昨日は子どものサッカー大会でした。小学校低学年の大会だったので二男がそちらへ、そして高学年の長男は別のところへ練習試合でした。私は車などの手薄な方へ行こうと思っていたのですが、コーチが「弟さんの方についてやってください」とのことでしたので、そうしました。会場は「２００２年ワールドカップ用に作られた競技場の・・・」と言うからそんなスゴイところでするのかなと期待したものの、「競技場の隣のグラウンドです」とのことでした。
まあそんなものかな、と思って行って見てビックリ！一面人工芝の立派なグラウンドでした。私どもの世代は人工芝というと、初めて後楽園球場に人工芝が張られたときのあまり良くないイメージ（怪我をしやすいとか疲労感が残るとか）があったのですが、今は非常にやわらかくて天然芝とほとんど変わらないのですね。こんなところで小学生のときからサッカーができるなんて、とても幸せなことです。試合の勝ち負けとは関係なく（ぼろ負けだったのです）、子ども達はとても良い経験ができたと思います。

それともなんですかね。子どもからしてみると、そんなグラウンドでできるのは当たり前みたいな感覚があるのでしょうか？もしそうだとすると、ちょっとウチの子にも釘を刺しておかないといけないかな、と思いました。で、コーチとそんな話をしていたら、コーチが言うには「ひと昔前とはグラウンド事情が大きく違って、今や芝生のグラウンドが結構たくさんあるので、むしろ子ども達にはそういう環境でたくさん楽しんで欲しい。」と。私などはケチな根性丸出しで「出し惜しみをして、もっとアリガタミを出した方がいいのでは？」と思ってたのですが、今はそのＷ杯の競技場が出し惜しみしているアリガタミのある競技場です、とのことです。

確かにここ数年で芝のグラウンドが格段に増えました。Ｗ杯の効果なのか、totoの還元金のお陰なのかは分かりませんが、サッカーに関わっている私にとってはとても喜ばしいことです。でも私の周囲では、「あの競技場のせいで県の財政を圧迫して給料が上がらない」と言われてて、とても肩身が狭いときがありまする。

今日はパクリです。いえ、今日もパクリです。何でもありなんです。イノミス「ドッグイアーの限界を探る」を見て、自分でもやってみたくなりました。

イノミスさんでは４連鶴まで折っています。私にはとても無理です。第一、普通の折り紙でさえ４連鶴など折ったことありませんし。

つい最近、あそびをせんとやさんのページに03年9月のリンクがあったので覗いてみたら、「ハミルトン路」の話に気付きました。正12面体とアリでウダウダとお話した内容は「ハミルトン路」というのですね。とても勉強になりました。しかも私が描いたものよりもすごくスッキリとした綺麗な形の平面グラフが掲載されています。まだ見ていない方もぜひご覧になってください。

先日、パズルショップtoritoでラッシュアワーというゲームを購入しました。混雑している駐車場から赤い車を出口から出すというゲームです。ただし、どの車も前後にしか動けません。ルールが単純だし駐車場も狭いので、大して難しくはないかな、と思っていたのですがこれがまたどうしてなかなか。

子どもと「あーでもない、こーでもない」とかやって楽しんでいます。上の２問はやさしい方の問題です。

この問題は難しい方の問題です。こちらのサイトでJAVAにて遊べるものを公開してくれています。

パズルショップtoritoがサイトをリニューアルしていてビックリしました。とてもセンスのよい感じになっているのですが、以前のものに慣れていたものだからラッシュアワーのページを見つけるのに手間取ってしまいました。

シンデレラ２のβ版をダウンロードしてみました。あまりよく使いこなせていないのですが、ひとつ載せてみます。

Javaをインタラクティブ作図用に使えるようにしてください。

左下の再生ボタンをクリックした後、点Aを三角形内でドラッグして放り投げてみてください。点Bも同様にやってみてください。見ているだけで飽きませんし、もっといろいろと楽しいことができそうですね。正規版が発売されれば購入したいです。阿原先生の解説本も期待しています。

昨日のシンデレラ２のサンプルページの中にこういうものがあって、この中の白い三角形は頂点をいろいろ動かしても正三角形みたいに見えます。「モーレーの定理」って角の３等分線ですよね。角の４等分でも正三角形になるのですかね？と思ったので、シンデレラで確認してみました。

Javaをインタラクティブ作図用に使えるようにしてください。

微妙に正三角形ではないようです。
ところで上のもののように角の４等分線だったら私でも作図できるのですが、角の３等分線をシンデレラで作図できたら「モーレーの定理」も確認できます。もちろん角の３等分線は定規とコンパスでは作図できないのですが、シンデレラだったらできるのです！（私はまだやってないのですが・・・）
詳しくは昨日のこちらをどうぞ。

昨日は子どものサッカークラブで親子サッカー大会が行なわれました。普段、高校生を相手に手玉に取られている私でも小学生相手なら何とかなるのでないかと思い、万全の準備を整えてきました。前日には高校のサッカー部でミニゲームに参加して体を慣らしつつも手玉に取られ、前の日の晩はイメージトレーニングをしながら寝たためによく寝付かれず、昨年の小学校の運動会で味わった肉離れを再びひき起こす悪夢にうなされながら当日を迎えました。
朝、悪夢にうなされながら目覚めると、なんと幸運なことに雨模様ではないか。こんなに激しい雨なら（実際は水溜りもできないほどの小雨でしたが、その時は大雨に見えた）当然中止だろう、と思ったのですが、事務局から入った連絡では「少雨決行」とのこと。ぬかるんだグラウンドでは普段の３％くらいしか実力を発揮できない。普段の３％だったら小学生相手でも片手でお手玉にされるかもしれない（”軽く手玉に取られる”と表現したつもり）。事務局に電話を入れて「こんな状況でサッカーなんかして怪我をしたらどうするのか。肉離れのつらさを分かっているのか。せめて人工芝のグラウンドで試合をさせろ。なんなら天然芝でもいいぞ。」と妻に訴えてもらいたかったところですが、阿吽の呼吸がいまいち伝わっていない。子どもたちから「これくらいの雨だったらできるよね」と聞かれて「うーん、どうかな。最近は酸性雨といってとても危険な雨らしいから。」と答えるのがやっとでした。
結局、集合時間を迎えて雨はあがり、仕方なく親子サッカー大会は開催されるのでありました。（つづく）

雨は上がったものの、気温は低く風の強い状況です。雨ばかり心配していたので、こんなに風が強いとは想定外でした。というのは私はひどい花粉症なのです。風が強い日は花粉がたくさん飛ぶためくしゃみと鼻水が止まらず、普段の力の２％しか出せないのです。くしゃみと鼻水をまきちらしながらドリブルして「近づくと鼻水がつくぞ」と脅す、という方法を思いつきましたが、それは私の美学に反する行為です。もうこうなったら仕方がない。正々堂々と小学生に胸を貸してやろうではないか。

試合前、監督が「保護者の体力を考えて、１０分間で区切って休みながらやりましょう」と言ってくれました。さすがスポーツ指導者である。見習うべきところが多い。ところが実際に試合が始まってみると１０分どころか３分間で体力が切れてきました。まるでウルトラマンみたいである。どうせウルトラマンに似るならスペシウム光線を出せるとか空を飛べるとか、もっといいところが似てほしいものです。
結局、グラウンド状態と花粉症のため３％×２％＝６％（正しいのか？）くらいの力しか出せませんでしたが、子どもたちと一緒にグラウンドを駆け回る楽しさを堪能できた良い一日となりました。父親の威厳を示せなかったのが心残りですが、来年の親子サッカーに向けて努力しようと思いました（花粉症を治すとか）。事務局をはじめ関係者の皆さん、お疲れ様でした。

１３日（月）の朝、外を見ると雪が降っていました。土日もこの時期にしては寒いなと思っていたのですが、雪が降るとは思っていませんでした。まあ、それでも３月の中旬ですから大丈夫だろうと思って、普通どおり出かけました。
毎朝、私のクラスの生徒の保護者と車ですれ違うのですが、いつものように会釈をしてすれ違った後、信号待ちをしているとその保護者がわざわざ車から降りてきて、「この先トラック同士が何台か離合で渋滞してますよ。回り道をした方がいいかも知れません。」と、親切に教えてくれました。とてもありがたいことです。そこで、少し戻って迂回路を通ることにしました。が、それが間違いのもとでした。

迂回路にはトンネルが２つあるのですが、一つ目のトンネルを抜けると一面真っ白。ゲゲゲっと思ったのですが、その迂回路も４、５キロのことだしまあ大丈夫だろうと判断して強引にノーマルタイヤのまま突き進んで行ったのですが、トンネルがあるような坂道ですし、進めば進むほど雪が積もっていたので、仕方なくチェーンを巻くことに。

これがその時の状況です。チェーンを片方巻き終わって、もう一本のタイヤのところに行ってみると、「シューー」という音がかすかに聞こえます。何の音だ？といろいろ探ってみるとタイヤにネジ釘が刺さっていて空気が抜けていたのです！タイヤをスペアに交換してもいいのですが、スペアにすると大きさが違うのでチェーンが合わない。万事休すと、JAFを呼ぶことにしました。携帯電話で＃８１３９（ハイサンキュー）に電話をするのですが通じない。よく見ると「圏外」の表示が・・・。雪山に遭難した気分でした。

その後、とにかく携帯のアンテナが立つところまで歩いて移動して、JAFに電話をして救援を待つことにしました。３０分くらいで着くという話だったのですが、４０分くらい待っても来る気配がない。再び電話をすると、途中で雪の深さに驚いてチェーンを巻いているところだとのこと。結局１時間くらいしてJAFの車が到着。処置をした後、誘導してもらいながら脱出しました。その２つのトンネルの間だけすごい状況で、トンネルを抜けるとなんともない普通の路面でした。JAFの方にお礼を言って、ガソリンスタンドでパンク修理をしてもらって、結局職場に着いたのが１０時半。しかもまずいことに職場付近では全く雪など積もっておらず、私の話を聞いても半信半疑の様子でした。

私が書くと嘘っぽくなってしまうのですが、これは実話なのです。決して遅刻の言い訳をしているのではありません。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---