昨日のようにうまく図が描ければもしかすると何とかなるのかもしれませんが、フリーハンドで描こうとすると至難の業です。そこで、下図のようなものなら描けるのでは・・・と思って描いてみました。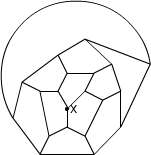

正十二面体とは似ても似つかないように見えますが、きちんと頂点は２０個、辺は３０本ありますし、一つの頂点に集まる辺の数は３本です。面が１１面しかないように見えますが、「囲まれた面」は１１個で「囲まれていない面」（図形の外側全部）が１個の計１２面ちゃんとあります。ただ、正五角形ではないし、外側の方の五角形なんてもう凸でもない、辺が曲線だ、などなど相当な無理があります。でも、この問題を考える時にはこの図で十分です。なんだかカブトガニみたいですね。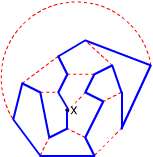
で、解答の一例を掲載します。

この図を見ながらだと、なんとなく解けそうな気がしてきました。次回へつづく。

昨日の正十二面体の平面モデルを見ていると、一筆書きの問題に見えてきます。ただし、「すべての辺を通って」という普通の一筆書きとは違って「すべての頂点を通って」元の位置に戻るという一筆書きです。スタートとゴールが一致する一筆書きで、しかも一つの頂点は一度しか通れないので、一つの頂点からは２本の辺しか出ることができません。つまり、頂点に集まる３本の辺のうち１本は使いません。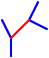
となれば、「どの２本の辺を通ろうかな」と考えるよりも「どの辺を使わないことにするか」ということを考えた方が考えやすいように思います。

で、上の図のように一本通らない辺（赤色）を決めれば、その両端から出る２本の辺（青色）は必ず通ることになります。それを考えながら、うまく数えていけば答えが出るはずです。

上のフラッシュ画像の再生ボタンを１度押すと頂点Xから赤い点線が一本出ます。この選び方は３本のどれを選んでも一様なので、後で３倍すればよいです。で、この赤点線が「使わない辺」を表しているとしますと、その両端の４本の辺は自動的に「使う辺」ということになります。でもフラッシュは自動的にはなってませんので（力不足でスミマセン）、もう一度再生ボタンをクリックしてください。
この状態で、次の「使わない辺」を選ぶときに場合分けが必要です。それぞれの青い辺の端から出ている２本の辺のうちの１本が「使わない辺」です。再生ボタンをクリックしてください。
仮に３のように選んだとしましょう。すると、次は自動的に青の辺が決まります。で、その後の番号４の時に次の赤い辺の選び方に場合分けが必要です。と言っても、そんなに多くはありません。
仮に番号５のように赤い辺を選んだとすると、あとは自動的に青い辺が決まり、一筆書きコースが完成します。

もうひとつ別のコースのものを作ったので掲載します。今度は２から３にいく時の赤点線の選択以降は一本道で決定します。

もっと鮮やかに計算でスパッと出せるものかもしれませんが・・・。私なりのアプローチということでこのような方法を紹介しました。次回は道順の一部を掲載します。

巡回コースの例を掲載します。昨日の平面モデルよりは正十二面体のイメージ図の方が見た目にわかりやすいと思いますので、そちらで作ってみました。

右と左で左右対称のコースになっています。これが「頂点Xから上向きの辺を使わない」ときのすべての場合です。その最初の使わない辺の選び方が３通り、それぞれのコースに右回りと左回りの２通りありますので、１０×３×２＝６０通りになると思います。

数学オリンピック予選の話に戻りますが、この手の問題１２問を３時間で解いて、今年の場合は７問正解で１次予選通過ということです。全問正解した者もいるというからビックリです。私のように手間ひまかけていては時間オーバーですね。もっともそれ以前に年齢オーバーでした。

正十二面体の辺に沿ってアリが歩く道順について考えてきました。一応答えは出たのですが、では他の正多面体だったら何通りになるのだろうか？と考えてしまうのは、自然の成り行きだと思います。そこで、問題を少しいじって以下のようにしたらどうなるでしょうか。

正多面体のひとつの頂点�]をとる。一匹のアリが�]を出発し、正多面体の辺上のみを歩き、�]以外の全ての頂点をちょうど一度ずつ通過して、�]に戻ってきた。アリの歩いた経路として考えられるものは何通りあるかを、それぞれの正多面体について考えよ。ただし、回転で重なり合うような経路や、道順が逆になっただけの経路も、異なるものとして数える。

・
・
・
・
・
・
・
・
・
・
少し間をあけて
・
・
・
・
・
・
・
・
・

正四面体の場合は６通り、正六面体の場合は１２通りになると思います。これらはひとつの頂点に３本の辺が集まっているところが正十二面体の場合と同じなので、同様の考え方で数えられます。では正八面体の場合はどうでしょうか？

・
・
・
・
・
・
・
・
・
またまた間をあけて
・
・
・
・
・
・
・
・
・

これはひとつの頂点に４本の辺が集まってくるので少し面倒です。集まる辺が３本のときは「使わない辺」を考えましたが、４本になると「使う辺」を考えても「使わない辺」を考えても労力は同じように思います。むしろ「使う辺」を考えた方がストレートで考えやすいでしょう。

隣り合う２辺を使う場合・・・・・

この３通りに、隣り合う２辺の選び方４通りと、逆順の２通りを掛けて３×４×２＝２４通り。

隣り合わない２辺を使う場合・・・

この２通りに、隣り合わない２辺の選び方２通りと、逆順の２通りを掛けて２×２×２＝８通り。で、合計３２通りになります。

正二十面体の場合ですが、何とかして答えを出せないものでしょうか？

	アリの経路	頂点	面	辺	ひとつの頂点に 集まる辺の数
正四面体	６	４	４	６	３
正六面体	１２	８	６	１２	３
正八面体	３２	６	８	１２	４
正十二面体	６０	２０	１２	３０	３
正二十面体	？？？	１２	２０	３０	５

正二十面体は、もうお手上げです。時間があるときにゆっくりと考えたいと思います。オイラーの多面体定理みたいにスパーっと出てくると気持ちいいのでしょうけれども。もし何かお気づきになりましたらご連絡をいただければ嬉しいです。

記述に間違いなどがありましたら遠慮なくご連絡をいただければとてもありがたく思います。

おとといの土曜日、２人の息子を地域のサッカークラブに初めて連れて行きました。何かスポーツをさせたかったのですが、なにしろ共働きの田舎住まいなものだから練習の送り迎えもままならなかったのでなかなか連れて行けなかったのです。息子たちは少し前までは結構やる気だったのですが、いざ、となると怖気づいたのか「やっぱり、やめとうこうかな」などと、弱気な発言をしていましたが、「行かないと警察に捕まるのだ」などとうそぶいて、強引に連れて行ったのです。
連れて行ってみると、やはり小学生ですね。すんなりとみんなも仲良くしてくれて、指導者の方々も歓迎してくれたので、練習後には「短パンとソックスがいる」とか言って、結構やる気になったので、ほっとしています。

昨日はいきなり練習試合だったので、「しっかりと球拾いとか後片付けとかをしてくるんだぞ」と言いながら連れて行ったのですが、指導方針が「試合の中で覚えていく」ということらしく、試合に出してもらっていました。試合自体はぼろ負けだったのですが、試合後「もっと練習せんと・・・」とつぶやいていたそうです。
とても雰囲気のよいチームで、指導者の方々も「小学生のうちは勝ち負けよりもサッカーの楽しさを教える」という方針だそうで、これには私も大賛成ですのでそんなチームに参加できてとても嬉しく思います。

私は試合をニコニコと楽しみながら見たのですが（指導者の立場よりはとても気楽でした）、妻は長時間寒い中で観戦することにかなり疲れた様子でした。

いつも楽しく拝見しているブログろくはロッパの･･･の２月５日の話題にルービックキューブが取り上げられていたのでそれに乗じて・・・というわけでもないのですが、私もいくつか持っていることを思い出したので、何回かに分けて紹介します。

左からルービックミニ、ルービックキューブ、ルービックリベンジ、ルービックプロフェッサーです。左から２番目のルービックキューブは１９８０年頃、はじめてルービックキューブが出回った時に買ったもので、作りがしっかりしていてまだまだ現役でしっかりと動きます。ルービックリベンジは妻が何かの時に買ってきてくれたもので、かなりチャレンジしたのですが未だ揃えきれずにいるのです。ですから、プロフェッサーは買ったっきり崩していません。ルービックキューブは買った当時（中学生だった）、３ヶ月くらいかけてできるようになりました。スピードを競う揃え方もあるようですが、私の場合は我流なのでとっても遅いです。まず８隅を揃えてから、次に辺の中央１２個を揃えていくのですが、自分のパターンがとても狭いのでそこまで持っていくのに時間がかかります。

職場に「この人は何の仕事をしているのだろうか」と思えるほどブラブラしている人がいます。なるべくかかわらないようにしていますが、「これでも同じくらい給料をもらってるのだろうな」と思うと少し腹が立ちます。どこの職場でも同じような人はいるのでしょうか？

忙しいと愚痴っぽくなって駄目ですね

ろくはロッパの･･･さんがこのサイトの名前を出してくれました。ありがとうございます。・・・と、冷静を装っていますが、「どひゃーっ」という感じです。嬉しいやらビックリやらを通り越して、すごい方が私のサイトを見に来てくれているのだなあ、と思うと身が引き締まる思いです。今後もどうぞよろしくお願いします。お教えいただいたJessica Fridrichのページを見に行きましたがなにせ英語のページなものですから時間がかかりそうなので、週末にでもゆっくり探検しようと思います。Don HatchさんのサイトのMagic cube 4Dもやってみました。これはすんごいですね。クリックしていくうちに元に戻せなくなってしまったのですが、変化していく様子を見ているだけでも楽しいです。ご紹介いただきありがとうございます。

さて、今日のキューブ（と言っていいのか？）は正八面体です。

これは見た目ほど難しくないと思います。と言っても、私の場合はガシャガシャまわしていると偶然「できた！」という程度のものですが。ただ、偶然にしてもできてしまうことから考えて、「難しくない」と言ってよいと思われます。3×3×3のルービックキューブは偶然でさえもできなかったのですから。

これは立体パズルの部屋の渡辺さんから購入したものだったか、それともネットオークションで手に入れたのだったか、ちょっと忘れました。まわし味が小気味良くて気に入っているもののひとつです。生徒に触らせて遊ばせたことがあるのですが、何度か壊してしまったことがあります（壊すというよりバラバラになった）。でも、これは道具なしでもすぐに復元することができ、その構造もとても面白いと思いました。
ルービックキューブ関連で感心するサイトをもうひとつ。立体パズル改造工房です。愛媛県の岡本さんのサイトですが、ご自身でルービックキューブを改造して見たこともないようなオリジナルのパズルを製作しています。私も「欲しいなー」と思うものがたくさん掲載されています。

ろくはロッパの･･･さんのお陰でとても嬉しくて気分晴れ晴れです。ありがとうございました。日記に愚痴を書くのは良くなかったですね。読んでくれている人まで嫌な気分にさせてしまったかもしれません。どうもすみませんでした。

今日は正四面体のピラミンクスです。

これは初心者向きです。すなわち私向きです。購入したその日のうちにできるようになりました。実感としては2×2×2のルービックミニよりも簡単なのではないかと思います（難易度を測る尺度がはっきりしないのですが・・・）。これはよく店頭でも見かけますし、手に入りやすいのではないかと思います。適度に難しくて、でも比較的簡単にでき、多くの人が達成感を味わうことができる、という観点から購入者が幅広く見込めるため商品として成り立ちやすいのでしょうか。
昨日の正八面体のものもそういう点からすると売れそうな気がするのですが。私の購入した正八面体のものは新品だったと思うのですが当初から箱がなくメーカーのロゴなどもないため商品名などがわからなかったのですが、昨日ここでも紹介した立体パズルの部屋で調べたところ、「Skewb Diamond」のようです。

毎年、年末に兄の家族と顔を合わすのですが、昨年末は６年生の甥にこの「Skewb Diamond」をプレゼントしました。一昨年はレインボーキューブ（後日紹介します）、その前はピラミンクス、さらにその前は２×２×２のルービックミニだったと思います。甥も興味を持ってくれて、これまでのものは全てできるようになったらしいです。それどころか、友達に教えてもらったりして４×４×４のリベンジや５×５×５のプロフェッサーまでできるようなことを聞きました。すでに私は越されています。

今日のものは正十二面体です。

Skewb Ultimateという商品名です。これを書きながら思い出したのですが、これと一昨日紹介したSkewb DiamondはMISDIRECTIONで昨年１０月に購入しました。当時はこのお店はまだ仮オープン中だったのですが、注文を申し込んだところ快く対応していただいて手に入れました。そしてこの２つは私が購入した途端に「在庫切れ」になってしまいました（スミマセン）。でも買い占めたわけじゃなく１個ずつ買ったのですよ。
その後、あそびをせんとやさんなどを通じてブログのMISDIRECTIONの存在を知ったのですが、偶然同じ名前のサイトなのだろう、くらいに思っていました。ところが、そのブログの左上に「オンラインショップ入口」とリンクが張ってあるではありませんか。もしや！と思ってクリックしてみると、やはり私の知っていたお店でした。世間は狭いものですね。
MISDIRECTIONさんにはご丁寧に素敵なクロスワードパズル入りの年賀状までいただいたのに返事を書いていませんでした。すみません。この場を借りて、明けましておめでとうございます。今後もよろしくお願いします。

私も中学生の時にクロスワードパズルの年賀状を自作して、友達に送った記憶があります。とても簡単なものだったのですが、全部を埋めるとある一列が私の名前になるように配置していて、その列のヒントに「天才少年現る」とか書いたと思います。それだけがために友人には「非常に難しいパズル」と評されました。

正十二面体の別物です。Megaminx というそうです。

これはシールが剥がれそうですし、何より一度崩したら２度と元に戻らないような気がして、購入して以来崩していません。せっかく良い物なのに、シールくらいもう少しキチンとしたものをすればよいのに、惜しいなあと思います。昨日までのものはシールも作りもかなりキッチリとしていて、まわし味がよいです。

話は変わりますが、いくつかのブログで数学を勉強する意味についての記述があったので、またまた便乗して私もひとこと。
なぜ数学を勉強するのか、という問いかけをこれまで何人もの生徒から問いかけられてきました。最近は「面白いから勉強するんだよ」と答えています。「何の役に立つの？」と問われたら「数学を役に立てるか立てないかは君たちのアイデア次第だ」と答えます。数学が役に立つかどうか、ではなくて、数学を役に立てるかどうかはその人次第、ということだと思うのです。役に立つ学問を学びたいというのなら、工学部や医学部を薦めます。それらの学問では、まず「役に立つ」「為になる」という観点があって、そのためには・・・という方向性です。ところが数学は最初から「役に立つ」という視点はないと思うのです。「役には立たないけど、面白そうだからこんなことを考えてみました」というのが最初で、次第に世界が広がっていく・・・という方向ではないでしょうか。広がっていく中で何らかのアイデアと結びついて「役に立つ」ということもたくさんあるでしょう。例えば、先日このサイトでも紹介した
カライドサイクルですが、一見何の役にも立たないように思えます。ところが、宇宙航空研究開発機構（ＪＡＸＡ）に見られるように、知っていれば素晴らしいアイデアと結びつく可能性だってあるのです。
私がもう少し若い頃には（今も若いのですが）「面白いから数学を勉強する」とは言えなかった。「でも先生の授業は面白くないじゃん」と言われて返す言葉もない自分の姿がイメージできたからです。今でも面白い授業ができているとは到底思えないのですが、年をとると（今でも若いのですが）開き直るというか、ずうずうしくなるというか。進学校に勤めていますが受験数学ばかりにならないように、気持ちだけは「面白さを伝えたい」ということを第１に考えているつもりです。

さて、立派なことを書いてきましたが、私は大学の数学についていけなくてドロップアウトした学生のひとりでした。当時は数学を「面白い」とは到底思えなかったです。ところが、ここ最近の話ですがあそびをせんとやさんやろくはロッパの・・・さんとか濱中先生のページなどに触れるにつけ、あらためて「おもしれー」と思える一方で「わかんねー」というジレンマがあって、そういう境界線にいる時に勉強したいという意欲が沸いてくるように感じました。

最近は自分の勉強不足を痛切に感じていまして、「内地留学」をしてみようかなともちょっと考えています。

今日は正二十面体です。Dogicという商品です。

これは昨年Meffertsによって再販されたものです。その前にVECSOというハンガリーの会社が開発したらしいのですが、そのオリジナルのものだったらオークションなどで１０万円近くの値がつくのではないでしょうか。そのオリジナルのものは、上の写真のように頂点で色分けされているものと面で色分けされているDogic２の２通りのDogicが販売されました。再販されたものはそれ以外にもいくつか色分けのタイプの違うものがあるようです。こちらのサイトで（スペイン語？）たくさん紹介されています。
この頃は物の紹介のみですみません。解き方については言及できません（私自身が解けないので）。

先週、運動部の顧問研修会が教育委員会主催で開かれました。前々から部顧問というのは報酬がないのでボランティアだという認識だったのですが、その研修会によると「賃金の面ではボランティアだが、事故などが起きたときには職務」として責任を問われる可能性がある、らしいです。これって、とんでもないことですよね。こんなことでは部顧問なんて引き受ける者はいなくなります。実際、立ち回りの上手な人は運動部の顧問など引き受けずに「好きな人がやればいい」とか言ってるくらいです。教育行政側も早急に何とかしないと、少子化も手伝って日本のスポーツシステムは崩壊していきますよ。

レインボーキューブです。

形は立法八面体です。左のケースに入っているものは各面の色が違って１４色バージョンで、右のものは対面の色が同色の７色バージョンです。これも難しそうですが、意外と簡単にできました。つくりもしっかりしていて、とてもよい品物だと思います。私はパズルショップtoritoで購入しました。toritoには先週末に注文した品があって届くのを楽しみにしているのですが、まだ入金してなかったです。明日入金します。またその品物についてもいつか紹介できるかもしれません。

話は変わりますが、土曜日にスポーツコーチサミットというものに参加してきました。講師は福島大学教授の白石豊先生です。白石先生はメンタルトレーニングの第１人者で（私なんぞが紹介するのもおこがましいのですが）先生の著書である「実践メンタル強化法」を読んだことがあり、「この講演は聴かないと後悔するな」と思って参加しました。とても聴きやすい語り口で、具体例と実践を交えた５時間の講演はあっという間に終わった感じです。中でも「プレッシャー克服法」と「感情のコントロール法」はスポーツの場面ばかりでなくいろんな場合に応用できそうで、非常に参考になりました。終わった後に講演録を送ってくれるようメールでお願いしたところ（講演の中で講演録の欲しい人はメールにてどうぞ、ということをおっしゃっていたので）、翌日には早速返信をいただきました。ありがとうございました。

今日はSquare-1です。購入した時からそろっていない（立方体でない）状態だったのですが、苦労の末完成しました・・・。

と言いたいところですが。

あと少しのところで完成に至っていません。ここまでこぎつけるのも偶然が重なったようなものなので、ここからチャレンジしても元に戻らないような気がして、この状態のまま２年が過ぎてしまいました。

大学の試験が終わって休みに入った、と卒業生が何人か高校に顔を見せてくれました。人によって様々なのですが、私が大学生の時よりも就職に対して危機感を持っているものが多いように感じます。私のときはバブルがはじける前だったので全体的に「何とかなるさ」という雰囲気だったように思います。今の大学生の方が遥かに大変かもしれません。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---