４つ重ねて回してみた動画も掲載します。

「right-angled kaleidocycle of order 8」４個重ね(96kb)

下は「right-angled kaleidocycle of order 8」の展開図です。PDF版はこちら。PDF版は例によって２段にしています。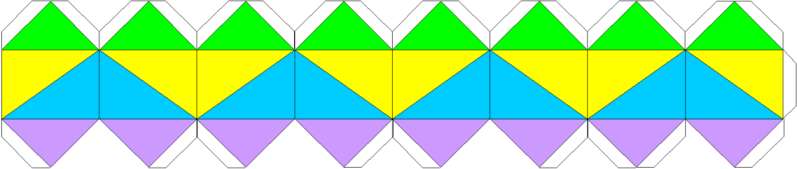

１：１：（ルート２）と１：（ルート２）：（ルート３）の直角三角形からできています。この立体は非常に面白くて、以前こちらでも紹介した吉本キューブにも関連してきます。吉本キューブにはNo.1からNo.3までの３種類があるそうで、そのNo.2だかNo.3だかにとてもよく似ています。No.2やNo.3は私も写真でしか見たことがなくてよくわからないまま書いているのですが、その辺りの話は次回にまわしたいと思います。

昨日は妻の誕生日で、ケーキを買ってみんなで食べました。ケーキを切りながらあそびをせんとやさんの「公平に分ける話」を思い出しました。我が家の場合は・・・、と言い出したら非常に特殊な話になって一般性のかけらもないのですが、基本的には私が切り分けて、選ぶときにジャンケンします。

このページの題名、「しごと・あそびごと・ひとりごと」について、その由来について問い合わせが殺到･････していないのですが、本当を言うとひとつも来ていないのですが、勝手に説明したいと思います。

「しごと」と最初にあるので「仕事熱心な人だろうなあ」と思う人もいると思いますが、そういう誤解は大歓迎です。ひらがなの上下に漢字と英語でルビをふっていますように（ルビと言っていいのでしょうか？）、「しごと」とは「私事」のことで、「仕事」ではありません。「わたくしごと」というと語呂が悪いので「しごと」と読ませています。
次の「あそびごと」には「work」と英語をふっていますので、「これが仕事のことか」と考えた方はかなりの仕事熱心であると言えます。「work」には「細工; 製作;〈集合的〉細工物, 作品, 製品, 特に手工品」という意味もあるようで（by 新グローバル英和辞典）、工作物などの話題を、というところから付けました（と言ってもあんなもので恐縮ですが）。
最後の「ひとりごと」については読んで字のごとく私のつぶやきみたいなものです。他人様がどう思おうが関係ない！私のひとりごとなのだ！という、孤独感にあふれた気合が込められています。「my Favorites」とありますように、私のお気に入りのものを話題にしようかと思っています。

手持ちのネタも切れつつありますので、今後は本当の日記のようになるかもしれませんし形態を変えるかもしれません。できるだけ長く続けられるとよいなあと思っています。

今日からちょっと変わった別の物体を紹介します。下の写真を見てください。

青と赤の立方体がそれぞれひとつずつ、なにか怪しげな切れ目が入っています。これ、実は輪ゴムでとめていまして、そうしていないとバラバラに崩れてしまうのです。さて、そこで問題ですが、バラバラになった後のパーツというかピースはどんな形をしているでしょうか？つづきはまた明日。

昨日の立方体、輪ゴムをはずして形を崩すと下の写真のようになります。

裏には別の色をつけています。

これは下図の赤い線で囲んだ四面体を２４個つなげて作ったリングです。これもカライドサイクルの一種と言ってよいかと思います。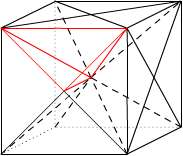

こんなにたくさんつなげると、前回紹介したカライドサイクルのように「クルクル回ります」と言っても「当たり前じゃん」という感じです。と考えると、前回のものは閉じるときと開くときを繰り返すギリギリの感じを不思議に思ったのでしょうね。今回のもののように開きっぱなしでは不思議でも何でもないですね。

このリングを「カライドキューブ」と名付けようかと思ったのですが、すでに「カレイドキューブ」という物があるそうですので、「k-cube」と呼ぶことにします。で、このk-cubeは組み方によって立方体以外の立体に変容します。つづきは次回に。

四面体を２４個つないだk-cubeのつづきです。２つを組み合わせると下のような立体にもなります。

	まず２つのk-cubeを揃えます。 前回紹介した四面体を２個 合わせてつなげたカライドサイクルができます
	うまく組んでいくと菱形十二面体ができます。
	さらに、またばらして組みなおしていくと、
	先程とは違った色の菱形十二面体ができます。 で、外側のk-cubeだけはがしていくと
	中には立方体が隠れていました。
	もう一度組みなおしていきますと、
	また別の色の菱形十二面体ができました。
	これも外側だけはがしていくと中には立方体が隠れています。

立方体をもうひとつのk-cubeで包むことにより菱形十二面体ができます。２つのk-cubeの立場を入れ替えれば別の色のk-cubeが作られます。また２番目の画像のように、２つが混ざったような菱形十二面体もできますので、今回の方法では合計３つのパターンで菱形十二面体に組むことができます（別の方法ならもっとたくさんのパターンで菱形十二面体ができます）。

次回はk-cubeの作り方を説明したいと思います。

今日はセンター試験です。受験生には普段の力をしっかり出し切ってほしいです。

k-cubeの展開図です。展開図といってもカライドサイクルのときのように一枚紙ではなく、バラした時の四面体ひとつ分です。PDF版はこちら。PDF版は６枚印刷して作成してください。

左の画像で、青い三角形が２：(ルート２)：(ルート２)の直角二等辺三角形、紫の三角形が２：(ルート３)：(ルート３)の二等辺三角形、緑の三角形が１：(ルート２)：(ルート３)の直角三角形です。以前も掲載した下の図をイメージして作りました。

これを一つ作るのは何てことはないのですが、一つのk-cubeには２４個必要ですし、二つ作るには４８個作らなければなりません。かなり根気の要る作業です。
つなげる時は、一番長い辺（２の長さの辺）同士と、一番短い辺（１の長さの辺）同士をつなげます。セロハンテープで表裏の両方から止めるとよいです。

カライドサイクルのようにつながった形で展開図が描けないかな、と考えて描いてみたのが下の図です。これを４枚つなげて一つのk-cubeができるはずです。破線の部分は切ってください。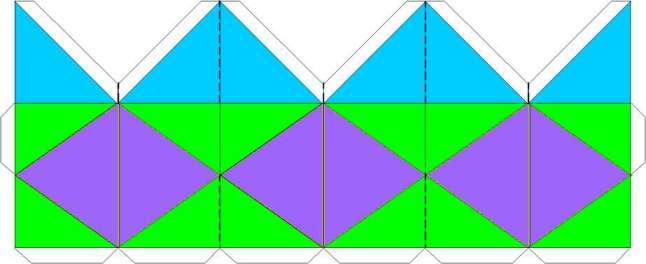

吉本キューブやカライドサイクルもそうなのですが、このk-cubeも内側のものが変形後には外側になったりするため、かなりキッチリ作ったつもりでも組み合わせた時にどうしても隙間ができてしまいます。仮に片方を少し小さめに作れば確かにきれいに収まるのですが、内側と外側を逆転させると全く収まらなくなってしまってうまくいきません。

k-cubeの最終回です。以前に「別の方法ならもっとたくさんのパターンで菱形十二面体ができます」と書きましたので、その「別の方法」を掲載します。

２つのk-cubeを組み合わせないで、それぞれが菱形十二面体の半分の形を作ることができます。上の写真では４面が緑色、４面がピンク、４面が半分半分になっています。

今度は切断面が平面ではなく、ギザギザになっています。３面が緑、３面がピンク、６面が半々です。

上の写真では６面が緑、６面がピンクで、半々の面はありません。

これは最初と同じように切断面が平面です。が、切断の仕方に違いがあります。５面が黄色、５面が紫、２面が半々です。

これらの他にもまだk-cubeには何らかの秘密が潜んでいるかもしれません。また、４面体のつなぎ方を変えたり、立方体の分割方法を変えたりしたら、もっと面白いことがあるのかもしれませんが、k-cubeについてはこれでひと区切りにします。

２２日はサッカー部の新人大会がありました。私の前々任校との対戦で、教え子の後輩が指揮を執っているチームだったのですが、延長の末２−３で負けました。両校の選手とも精一杯の力を出し切った好試合だったと思います。私も非常に疲れました（その前の試合で線審をしたりしたので）。もう"年"ですね。

ここ２、３日はセンター試験のデータ処理や成績資料作りが大変です。２２日に試験が終わり、２３日に自己採点をして、昨日（２５日）に予備校等の受験産業から出されるデータを収集して２７日に行なわれる校内の会議に間に合うように資料を作ります。生徒一人ひとりの最適な進路を模索して、一人の教師の判断に頼るのではなく皆で知恵を出し合おうという会議です。

それにしても受験産業のデータ収集・発信の能力というものはスゴイです。コンピュータとインターネットの普及によって、大学受験も大きく様変わりしました。私が高校生の時は、非常に乏しい情報の中で自分と先生の「勘」とか「感覚」で大学選びをしていたように思います。今では大学入試も非常に複雑になったため、「感覚」に頼っていたら大失敗をします。例えば、傾斜配点といって大学ごとにセンター試験の点数を自由に重み付けがなされていますし、センター試験と２次試験の点数配分も大学によって違います。国公立大学だけをとっても「前期日程」「中期日程」「後期日程」のように複数の大学を受験可能ですし、推薦入試制度などもあります。それに加えて私立大学の入試となると・・・。もう、「感覚」で捉えられる域をはるかに超越しています。生徒も教員も受験勉強だけでも大変なのに、「大学選び」という観点からも情報収集し勉強しないといけません。こういう状態ってどうなんでしょうね？

例えばセンター試験を１１月くらいに早めて２次試験までの期間を長く取るようにしたらもっとゆっくりと判断ができるのに、などと思います。あるいは入試制度をもっとシンプルにできないものか、とも。

とにかくこの時期、いろんな人がイライラしていてあまり良くないです。

これ、何だかわかりますか？

テレビの画像ではないです。おまけにもうひとつ。わかった方は気分を害さないでくださいね

答えは次回にします。

昨日の画像、少しカメラを引いて撮影すると下のような感じになります。

ピンをたくさん並べて作られたスクリーンです。ピンの上下方向の動きが自由になっていて、上の画像のように手の形をとったりすることができます。

私が持っているものは「Pin Artist」という商品名で、台湾製です。７ｃｍ×１０ｃｍくらいの長方形なので、あまり大きなものは形取れないのですがなかなか面白いです。インターネットで「ピン・スクリーン」などのキーワードで検索すると、科学博物館のアトラクションの一つとして大きなものが展示されているところもあるようです。

このおもちゃは二男のお気に入りで、よく自分の顔の型をとったりして遊んでいます。私も顔を形取ってみたのですが、何度取ってもグロテスクなものになってしまってとてもネット上に掲載できるものではないと判断し、手の形を掲載するにとどめました。

このおもちゃ、「トイ・ストーリー２」という映画の中で一瞬だけ登場する場面があります。もう少し広い面のものが欲しいなあと思うのですが、どこに売ってるものなのでしょうか？私が持っているものは、たまたまネットオークションで手に入れたものです。

最近、面白い問題を見ましたので紹介します。

正十二面体のひとつの頂点�]をとる。一匹のアリが�]を出発し、正十二面体の辺上のみを歩き、�]以外の全ての頂点をちょうど一度ずつ通過して、�]に戻ってきた。アリの歩いた経路として考えられるものは何通りあるか。ただし、回転で重なり合うような経路や、道順が逆になっただけの経路も、異なるものとして数える。

これは先日開催された数学オリンピック予選の問題です。数学オリンピックとは高校生以下の数学好きな生徒を対象に行なわれる国際大会で、４０年前から開催されています。今年はスロベニアで行なわれるらしいです。対象が「高校生以下」なので高校数学までの知識ですべて解けるはずの問題が出題されるのですが、上の問題を見てもわかるように難問揃いです。
上の問題は予選の10番の問題ですが、いかがでしょうか。その筋の方には（どんな筋や）簡単に解けるものなのでしょうか？私なりのアプローチを試みて、何回かに分けてこの場で取り上げようと思います。

なかなかイメージがわかないので、正十二面体の図を作ってみました。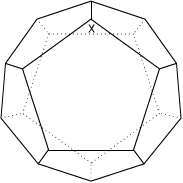

こんな図を見てもなかなか難しいです。実際私の場合、正十二面体の紙模型（だいたい手近に置いてあるのです）を見ながら考えたのですが、そんな立体図形を手にとって考えても一つの経路を辿ることもできませんでした。ひょっとしたら、そんな経路はないのではないか？とか疑ったりしたのですが、ちゃんと経路はあります。一例を掲載しますね。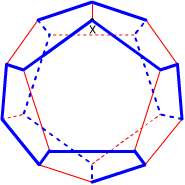

青の経路が一例です。逆回りも異なるものとして数えるので、これで２通りです。次回もこの続きを。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---