先週の土曜日に「青少年のための科学の祭典」が近くで開催されたので、子連れで行ってきました。私の住まいの周辺は自然には大変恵まれているのですが、文化的な施設などはやっぱり都会に集中するみたいなのでこんな催しが近くで開かれるのはとてもありがたいです。

科学の祭典の看板です		光が虹色に見えて綺麗でした
とても丁寧に教えてくれました		綿菓子作りです

我が子は真っ先に綿菓子作りに走りました（育ちが分かりますね・・・）。田舎ではありますが、かなりの親子連れで賑わっていました。

かなり賑わっています

手元に戻る紙飛行機作り

子ども達も夢中で工作に取り組んでいました。関係者のみなさん、ありがとうございました。

「あそびをせんとや」さんでバージョンアップした「キングと悪魔のパズル」にはまってしまいました。このパズルそのものも非常に面白いと思うのですが、プログラムもすごいと思います。なかなか勝てません。。。

簡単なハトメ返しの例をいくつか作ってみました。

「あそびをせんとや」さんでバージョンアップされた「キングと悪魔のパズル」の「思考ルーチン視覚化アプレット」を作者のhhaseさんからいただきました。ありがとうございました。これ、ホントにすごいです。次は出来るだけ少ない手数で勝てるように挑戦してみたいと思います。

「あそびをせんとや」さんに公開されている「キングと悪魔のパズル」のもともとの発案者はConwayという数学者だそうです。

このConwayという数学者の名前を以前にも聞いたことがあって思い出したのが「スプラウト」というゲームです。もうずいぶん昔（10年以上前）に図書館の古い本（何という本だったか忘れましたが）でこのゲームを知ったのが最初で、当時はまだ必勝法が見出されていないと書かれていたのを覚えています。「遊びの博物誌１」（坂根厳夫著、朝日新聞社）では、スプラウトの発案者の一人が数学者のジョン・コンウエイであると記されています。ルールを簡単に説明します。

１．紙と鉛筆を使って２人で遊ぶゲームです。

２．紙に点をいくつか（３〜５個くらいが最初は適当と思います）書きます。

３．先手の人が点から点を線で結び（点から自分自身に戻ってきてもよいです）、その線上に点を一つ書き加えます。

４．後手の人も同様に線を引き、点を打ちます。その際、線が交差してはいけません。

５．一つの点から出ていく線は３つまでです。ですから、新たに打たれた点はあと一本しか線を結べません（もともと線上にあるので）。

６．先にその操作が出来なくなった人が負けです。

下図を参考にしてください。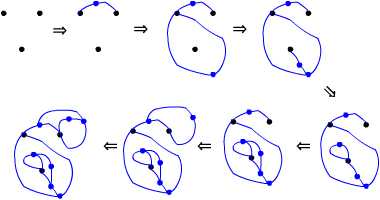

この例では先手が勝ちです。しかし、同じ３個の初期設定でも下の図では後手の勝ちです。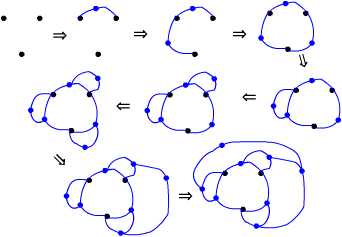

「Sprouts」には「芽生え」とか「萌え」（今年の流行語ではないですが・・・）という意味があるそうです。確かに芽生えて膨らんでいくような感じがします（私のアイデアは膨らまないのに・・・）。

昨日のスプラウトの画像をFlashにしました（対戦はしてくれませんが）。

上のものだと後手の勝ちです。が、下のものになると先手の勝ちです。

最後の状態で赤い点からは２本の線しか出ていません。これを不飽和点と呼ぶことにします。最初の点が３個なら、それらから計９本の線が出ることができます。この状態を９ポイントと呼ぶことにすると、点を結んで線を引いた時点で２ポイント減りますが線上に点を打つことにより１ポイント増えて、−２＋１＝−１ポイントということになります。先手の第１手目が終わった状態で８ポイントになったわけです。その後も同様に１ポイントずつ減っていくので、勝敗は最後の不飽和点の数によることになります。下図のようにうまく点を囲い込んで、不飽和点を偶数個残すか奇数個残すか・・・というところが勝敗の分かれ目になってきます。

最近ではテレビゲームやコンピュータゲームが流行していますが、このような紙と鉛筆だけで出来るような素朴なゲームもいいと思うのですがどうでしょうか？

スプラウトというゲームを最初に知った本にはもうひとつ「ブリュッセル・スプラウト」というゲームも紹介されていました。これはほとんどスプラウトと同じなのですが、

１．点ではなく、＋をいくつか紙に書く。

２．＋の短い線分（−と｜）の端点から別の端点へ線を引き、その線上に短い線分を引く（スプラウトで線上に点を打っていたような感じ）。

３．ひとつの＋からは４本の線が出ることができます（スプラウトの場合は３本だった）。

４．線が交差してはいけません（これはスプラウトと同じ）。

５．先にいけなくなった人が負けです。

例によってFlashを作ってみました。

ちょっとやってみたら気付くと思うのですが、このブリュッセル・スプラウトは最初の＋の数により先手必勝か後手必勝が決まっています（ので、ゲームになりません）。最初の＋の数がｎ個なら、どのようにつなげても（５ｎ−２）手で終了します。

スプラウトの場合は線をつなげて点を打てば１ポイントずつ減っていったのに対し、このブリュッセル・スプラウトは線をつなげて−２ポイント、線分を打って＋２ポイントなので終わらないのではないか・・・と最初は考えたのですが、ちゃんと終わるのは不思議な感じがします。

１週間ほど出張に出るので更新が出来ません。HP公開１ヶ月にして挫折の危機！ですが、１週間後からまた再開したいと思います。

出張から帰ってきました。ＨＰの更新をしようと、まずはこのページを開いてビックリ！カウンターが留守の間にもかかわらず５０以上も増えていました。見に来てくださっていた方々にはご迷惑をおかけしました。また、見に来てくださってありがとうございます。「誰かが見に来てくれている」ということを励みにして今後も続けていきますのでどうぞよろしくお願いします。

北海道への出張でした。いくつか差し支えない程度に写真を掲載します。

写真だけ見ると遊びに行ったみたいですね。ちゃんと仕事もしました。とても疲れました。

いつも出先で困るのはお土産です。大人への土産は「なんとなく・・・」でもいいかなと思うのですが、子どもへの土産は何にしようか迷います。特に男の子なので装飾品には興味がなさそうだし、地酒というわけにもいかず、結局北海道とは何の関係の無いものを買ってしまいました。これじゃ単なるプレゼントですね。

出張中、いくつかアイデアがわいたので今日（代休）はそれをここに載せる準備をしたいと思います。

１１月２９日にハトメ返しについて述べましたが、それは５年前の秋山仁先生の講演がきっかけでした。その後、実は昨年の夏にも秋山先生の講演を聴く機会があり、そこで紹介されたのが立体ハトメ返しでした。平面のハトメ返しが三角形や四角形を分割・再結合することで別の図形になったように、立体ハトメ返しは立方体や直方体などを分割・再結合して別の立体が作られます。「知性の織りなす数学美」(秋山仁著)に詳しく書かれていたので、マネをして作ってみました。

わかりづらくてごめんなさい。上の例では、立方体２つ分の直方体（赤色）が菱形十二面体（黄色）に変化しています。

次回以降、もうちょっと作ったものがあるのでそれを紹介したいと思います。

昨日の立体について少しだけ説明をします。昨年の秋山先生の講演で遠くから見たときにはよくわからなかったのですが、とにかく立方体２つ分の直方体が菱形十二面体にパタパタと変化したことだけ覚えていました。家に帰ってからデジカメの写真を確認して、下図のような切れ目が入っていることが分かりました。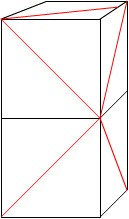

私は考えてから行動するタイプではなく、考える前に行動してから後悔するタイプの人間ですので、とりあえずその辺にある空き箱（確かスーパードライだった）を切って立方体を組み立て、デジカメ写真で確認した切れ目通りに真っ直ぐ切った立体を作ってみました。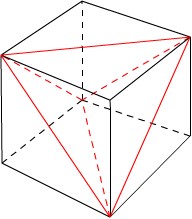

図の赤い線で切った立体は、確かに外側からは講演で見たものと同じなのですが、当然ながら内側に空洞ができます。この空洞は、今思うと当然なのですが正四面体です。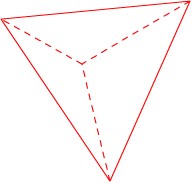

それに気付けば、その正四面体の（内接円や外接円の）中心と各頂点を結んだ線で正四面体を４つの合同な三角錐に分割して、外側の三角錐と合体させれば空洞ができないはずです。

上の右側の立体を８個作り、うまくつなげて完成しました。できたときは非常に嬉しかったのですが、なにせスーパードライの空き箱ですしみんなに見せるには恥ずかしい出来栄えだったので、気合を入れてアクリル板でもう一度作ってみました。（昨日のFlash画像はアクリル板のものです）

その後、詳しい作り方が「知性の織りなす数学美」(秋山仁著)に書かれていることを知りました。自分で作ってみようと思われる方は一読をおすすめします。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---