「シンデレラ」という本を購入しました。童話のシンデレラではなく、幾何図形をコンピュータ上で作図するためのソフト付属の解説書です。というより、作図ソフトに丁寧な解説書がついているような、そんな本です。
シュプリンガーフェアラーク東京社から購入しました。が、amazonなどでも購入できます（むしろそちらの方がお薦め）。
このソフトを使うとJAVAの知識がなくても簡単に作図の練習問題が作れるので、私も挑戦してみました。
こちらのサイトでもっと専門的なサンプルが見られます。

垂直二等分線


線分の三等分


三角形の外接円


２点を通り直線に接する円(難)

長男が２歳の頃に買った積木をお菓子の空き箱に入れているのですが、実はちょっと無理があって、きっちり詰めようとすると６個だけほんの少しはみ出してしまうのです。

箱は約２０センチ×２０センチ×６センチ弱の直方体で、積木は一辺３センチの立方体ですが、２段にするとほんの少し上にはみだしてしまい蓋を閉めることができませんでした。

浅知恵で、斜め向きに敷き詰めてみるとうまくいくんじゃないか、と思ってやってみたのですがやはり６個埋まりませんでした。（下の写真。わかりにくくてスミマセン）

２段目は中途半端だけど結構すき間が広いので、このスペースを利用できるように入れられないかと考えた末、下の写真のような入れ方を考えました。（わかりづらくてスミマセン）

入れ終わったときには何か嬉しい気持ちでした。

最近、私のクラスの生徒が「Attack Island（アタックアイランド）」というボードゲームを持ってきて遊んでいたので、私も試しに生徒と対戦しました。完敗だったとです。ヒロシです。その後、ある先生から「生徒がこんなもので遊んでましたよ」と、そのゲームを渡されたとです。立場がなかったとです。

負けたのが悔しかったので、「研究してリベンジしてやる！」と見栄を切ったものの、研究が進んでいない状態です。

どのようなゲームか、少し説明します。

ルール

１．８×８のマス目（オセロと同じ）の盤上に自分と相手の駒が一つずつ乗っています。

２．駒はその周囲８箇所に動くことができます。

３．自分の手番では、まず自分の駒を動かし、次に空いているマス目を一つだけつぶします。（「つぶす」とは、お互いそのマス目には行けなくなるということ。ボードゲームではマス目を押し込めるようになっていたのですが、オセロ盤でやるときにはオセロの白黒の石を置くようにすればよいです。）

４．駒のまわりをつぶされて、先に行けなくなった方が負けです。

最初はオセロ盤で子どもとやってみたりしていたのですが（これも勝ったり負けたり・・・）、コンピュータ上でできないものかと思い、エクセルでシュミレーションみたいにできるよう作ってみました。

最初はこの位置から

黒のマスはつぶせません

黄色の勝ちです

いつも楽しく拝見しているあそびをせんとやさんに紹介されている「Posit」というゲームの簡易版という感じで、低年齢の子どもにもすぐ理解できるルールだし対戦時間も短くてすぐ終了するので、おすすめです。

この続きはまた明日ということにします。

８×８の盤だと私には難しすぎるので、２×２の盤でやってみることにしました。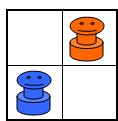

これだと先手がどうあがいても（あがきようもないのですが）後手必勝です。では、３×２の盤ならどうでしょうか？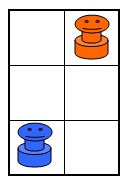

実際にやってみるとすぐわかると思うのですが、下図のようにこれは先手必勝です。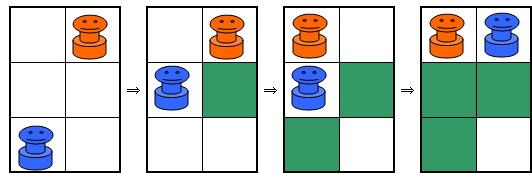

ところが、同じ３×２でも最初の配置が違うと後手必勝になります。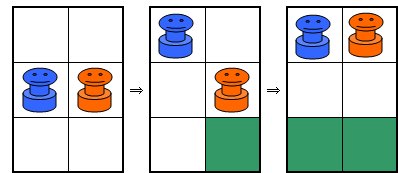

上図の状態で２×２の状態になったため、後手（赤）必勝となります。最初の配置によって先手必勝か後手必勝かが分かれる点も興味深いです。

３×３だと、私の試行錯誤によると先手必勝となります。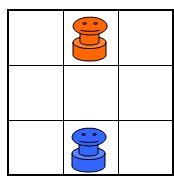

その他４×３や４×４などで考えてみても面白いと思います。

私の推論では、まずこのように盤が狭いとき、（１）偶数個のマス目（２×２や４×３）の場合は後手必勝、（２）奇数個のマス目(３×３など）の場合は先手必勝、になるのではないかと思います。３×２で先手必勝となるのは例外だろうということで。。。

この推論もお互いが対等の状況から始めたときの場合です。問題点は「盤が狭い」とは正確にはどのような場合か、３×２で先手必勝となるのは本当に例外なのか、などなどたくさんあると思いますが・・・。

また、盤が広いときは、ゲームが進んで（１）お互い同じ領域内に閉じ込められたとき、と（２）それぞれ違う領域に閉じ込められたとき、に分けられて、（１）のときは上記のとおり、（２）のときはより領域が広い方が勝つのではないでしょうか。

私の場合、もうちょっと試行錯誤が必要ですね。

「日々日記」というフリーソフトを使ってみることにしました。私のような無精者は４日目にして「めんどくさい」モードに突入しつつあります。そこで、この「日々日記」。とってもシンプルお手軽で、すぐに操作にも慣れました。しばらく使ってみてまたいつかご報告します。

最近は進路指導部関連の資料をエクセルで作っています。骨の髄までめんどくさがりの私は、来年も同じめんどくさい作業をしなくてすむように、色々と配慮して作っているつもりです。最近の私のモットーは「自分が楽をするためならどんな苦労も惜しまない！」

もうすっかりコンピュータのリバーシには勝てなくなってしまいました。これも先手必勝とか後手必勝とかがすでに読み切られてしまっているのでしょうか？

Attack Islandのシュミレーションをエクセルで作ったついでに、リバーシもエクセル上でシュミレーションできるようにしてみました。ダブルクリックで●、右クリックで○が表示されます。（右クリックメニューが表示されて邪魔、などの問題はあるのですが・・・）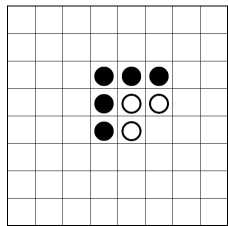

さらについでに、４×４バージョンも作ってみました。これは後手必勝のようです。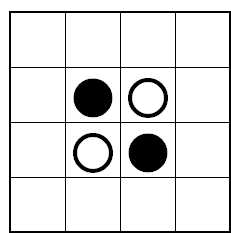

さらにさらに、Positもシュミレーション出来るように作ってみました。ダブルクリックすると色が３段階で濃くなっていきます。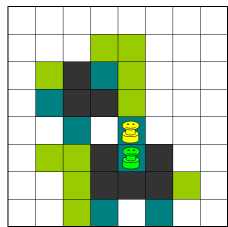

M先生、本日は色々とありがとうございました。早速光が丘中学のHPを見ました。とても参考になりました。こちらが「日本の学校・更新頻度ランキングリスト」のページで、こちらが「zphoto」のページです。御校は県内トップですね！さすが！！＾＾

１年くらい前、吉本キューブなるものの存在を知りました。１９７１年に吉本直貴さんが考案した立方体の幾何学オブジェです。詳しくはこちらのサイト「幾何学おもちゃの世界」をご覧ください。

私の場合、写真やイラストを見てもあまりピンとこなくて、どうなっているのだろう？？ということで、紙工作で自作したりしてみました。自作モノはまたいずれ紹介したいと思います。

今日は先日手に入れた本物（本物ってなんだ？）の吉本キューブをアップします。

立方体８個を「無限に回転する立方体」と同じ連結方法でつないでいるにとどまらず、さらに立方体の内側から星型の立体が取り出されます。生徒に見せると「もやっとボールだ」と言っていました。さらにはその「もやっとボール」を包んでいた入れ物の立方体自体も「もやっとボール」になります。

一見立方体にしか見えない物が全く別物になってしまうという不思議さ、内側が外側になり外側が内側になる構造など非常に興味深い立体です。

ダイソーでぶらぶらしていたらこんなパズルを見つけました。

よく見ると吉本キューブの「もやっとボール」と同じ形をしています。吉本キューブを手作りしたときに思ったのですが、この形は空間を隙間なく埋め尽くすはずです。それを実際やってみるために、このパズルを５個買ってみました。吉本キューブを５個作るのはしんどいので・・・。

家に帰って実際に組み合わせてみました。

こんなにイガイガのでこぼこなのに空間を充填するのも不思議な感じがします。

先日紹介した吉本キューブは最近購入したものですが、下の物は購入する以前に紙で作った吉本キューブです。

⇒
⇒
⇒
⇒
⇒

私は紙工作をするときによく使う紙はゴッホ画用紙です。厚すぎず薄すぎず、加工しやすいし値段も安いです。展開図をパソコン上で作成してプリンタで出力すればとても手軽に同じものがいくつも作れます。下に展開図を載せてます。８枚印刷してご使用ください。

吉本キューブのパーツ展開図

昨日の吉本キューブの写真では面白さが伝わりにくいと思ったので、下にFLASHで動いているように見せかけてみました。

FLASHは不慣れなものでギコチナクなってしまいました。

画像がうまく表示されない方は、こちらからFLASH PLAYERをダウンロードしてください。

調子に乗って、こんなものも作ってみました。

吉本キューブもそうでしたが、立方体を合同に２等分したものを単位としてそれを８個つなげたもので１個の「もやっとボール」ができるわけですから、別の２等分の方法で違ったタイプの吉本キューブができます。上の絵では立方体が切頂８面体２個に変身しました。

昨日紹介した切頂８面体型の吉本キューブの展開図を公開します。４枚同じものを印刷して組み立ててみてください。

切頂８面体型吉本キューブの展開図

同じ立体でも色々な展開図が考えられると思うのですが、実際に色々と作ってみると私なりに考えるところがあります。まずは、やっぱり作りやすいものがいいです。ハサミやカッターの入れ方が複雑になるとミスも多くなるだろうと思いますし、面倒です。また、のりしろの入れ方についても少し工夫すると作りやすくなる場合があります。先日掲載した吉本キューブの展開図(再掲)では、のりしろのない三角形を最後にのりしろに向かって蓋をする感じで組み立てると、セロテープを使わずに作ることが出来ます。

また、用紙を効率よく使うにはどの展開図が最適か、どのように配置したらよいのか、なども考えます。例えば上の切頂８面体の展開図の場合４枚の用紙が必要ですが、こちらの展開図なら同じ大きさなのに３枚ですみます。

このような中にも数学が潜んでいるのでは・・・と感じています。

TOM CUBEとは、戸村浩氏発明の立方体おもちゃです。詳しくは「幾何学おもちゃの世界」をご覧ください。こういうものを見ると、どうしても自分で作ってみたくなったので、夏休みに子どもと一緒に作ってみました。

画像ではわかりにくいので、デジカメの動画で撮影してみました。

トムキューブの動画

動画でもわかりにくかったかもしれません。立方体８個で相似比２倍の立方体を作っている点は吉本キューブとよく似ているのですが、吉本キューブは立体の辺同士を連結しているのに対し、TOM CUBEは頂点を連結しています。

トムキューブは８個の立方体を頂点でつなげて作成します。つなげ方は下図を参考にしてください。見えないところは見えている部分と対称と考えてください。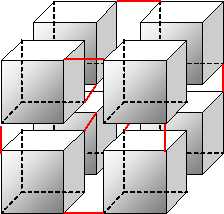

⇒

⇒

夏休みに長男の貯金箱の工作として一緒に作ったのですが、二男も作りたいというので、またまた一緒に作りました。大雑把ですが、写真を掲載します。

⇒ 道具はこんな感じ	⇒ 連結用の紐(5mm程度)	糊付け前に
⇒ 紐をかませます	⇒ 4つつなげたところ	下半分ができました
⇒ 上半分も同様に	⇒ 二男のリクエストで	カービーにしました
⇒ もう一面は	でんじゃらすじーさんです

昨年の文化祭で「爪楊枝点描画」をクラスで作成しました。

今日はそのときの様子を掲載します。

90cm×90cmのスチロール板に	爪楊枝を刺していきます
疲れてこんなひとコマも(針のむしろ？)	完成しました！！

明日はこの設計図についてを解説します。

モザイク画の設計図についてです。まずは元になる画像を決定して、サイズを変更します。今回の場合は270cm×270cmのスチロール板に1cm間隔で爪楊枝を刺して作成するので、画像サイズは270ピクセル×270ピクセルとします。次に、減色します。フルカラーだと何万色も必要で実際には無理なので、多くても16色以内に減色します(今回は8色でした)。私はPaintShop Proを使いますが、PhotoShopなどでもサイズ変更や減色ができます。

⇒

減色した画像は270×270の点で作られています。その１点１点の色情報（RGB値）を取得できれば、ほぼ設計図はできあがります。そのために簡単なソフトをVisualBasicで自作しました。そのことについてはまた後日紹介したいと思います。
その自作ソフトではRGB値をcsvファイルに保存するようにしていますので、そのまま起動してExcelで設計図を作っていきます。ところがExcelは２５６列までしかありませんので、２４０列で一旦止めて残り３０列はその下に表示するようにしています。

まだRGB値のままです。

⇒

ctrl＋ｈで置換します。

RGB値のままだと分かりにくいので、Excelの置換機能を使ってアルファベットに置き換えていきます。今回の場合は８色だけなので８回置換すればＯＫです。

Ａに置き換えたところ

⇒

置き換えたら列幅を揃えます

列幅を最適化するとおおよそセルが正方形になりますので、表示倍率を２０％にして全体を表示させると、下図のようにまるで写真みたいに表示されました。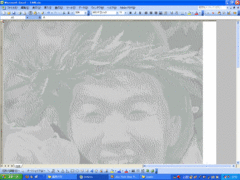

はじめてこれを見たときには驚きとともに感動しました。
次回は自作ソフトについて紹介します。

RGB値を取り込む自作ソフト「画像行列」（変なネーミングですが・・・）を紹介します。Visual Basicで作成しました。それまではExcelのVBAは扱ったことがあるのですがVBは初めてで、これが初めて作成したプログラムです（そしてその後はこれっきりなので、最初で最後かも）。

起動すると下図のような画面が現れます。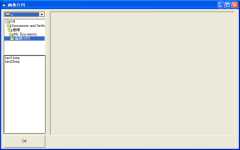

左上のボックスで画像元のフォルダを指定し、左下のボックスから右のスペースに画像ファイル名をドラッグ・ドロップすると、下図のように画像が表示されます。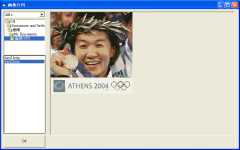

左下の「OK」ボタンをクリックすると下図のようなメッセージが表示され、これで作業は終了です。

元画像と同じフォルダに「test.csv」という名前で、RGB値を並べたファイルが作成されました。

興味のある方はメールでご連絡ください。

５年ほど前、数学者の秋山仁先生の講演を聴く機会があり、その中で興味をそそられる話がなされていたのでここで紹介します。まず、下のFlash画像を再生してみてください(正方形の左上のボタンをクリックしてください)。

赤枠の正方形が青枠の正三角形に変身しました。温泉宿などにあるタングラムパズルのようですがこの図形にはちょっと制限があって、辺か頂点上に蝶番のように可動だけど離れない点があり、そこをハトメパンチで固定したようにしてクルクルと変形していきます。これをハトメ返しというそうです。この正方形⇔正三角形の変形は天才パズリスト・デュードニが「カンタベリーパズル」の中で紹介したのが最初だそうで、秋山先生はこの図形分割のことを「デュードニ分割」と呼んでおられました。詳しくはこちら「知性の織りなす数学美」(秋山仁著)をご覧ください。

さて、このカンタベリーパズル、どのような比で分割すればうまくできるのでしょうか？

自宅に戻ってこのページの更新作業を使用と思ったら、なんとカウンターが倍増していました。昨晩が５０くらいだったのに今は１００を越えています。これまで２〜３人にしかURLを教えていなかったので、毎日カウンターは２〜３ずつしか増えていませんでした。２０日くらいかけて５０（というのも情けない話ですが・・・）だったのに、１日にして倍増！びっくりしました。

が、その後「あそびをせんとや」さんのページを見て納得しました。なんと、「あそびをせんとや」さんのページでここを紹介してくれていたのでした。ありがとうございます。これからも一層（でもぼちぼち）がんばるぞ！とファイトが沸いてきました。「あそびをせんとや」さんからお越しの皆さん、はじめまして。今後もどうぞよろしくお願いします。

昨日のハトメ返しの続きです。５年前初めてこの図形を見た後、自宅に戻ってから自分で作ってみようと思って厚紙で作ったのが左下の画像です。右の画像（昨日のものを再掲）と比べてみてください。

４辺とも中点をとって分割してみたら、このようなものができました。最初は「できた！」と思ったのですがどうも様子がちがう。よく見ると正三角形でなく二等辺三角形になってしまいました。三角形のときの赤い切れ目も、講演会で見たときは段差があったはずなのにこれは十字になっています。そこで、色々と考えたあげくに出た答えのみ掲載します。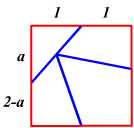

上図のように正方形の一辺の長さを２とすると、上下の辺は中点で分割されることになります。左の辺を図のように分割したとすると、

	となります。で、これは
	と非常に似通った数字です。

上の式は正確な値でそれはそれで価値のあることなのですが、実際に作図したりするときに使える数字は下の式です（作図誤差の範囲としました）。一辺の長さが２なので結局左の辺を４：３に、右の辺を３：４に分割した点を利用すればよいです。

計算して上の値が出た後何か簡単な比にならないかと考え始めたら、すぐにこの比が見つかりました。こんな簡単な比の近似値が存在するのも不思議な感じを受けました。

このページは（他のページと同様）リンクフリーです
ご意見・ご感想をお聞かせくださいtetetetessy@@gmail.com

---